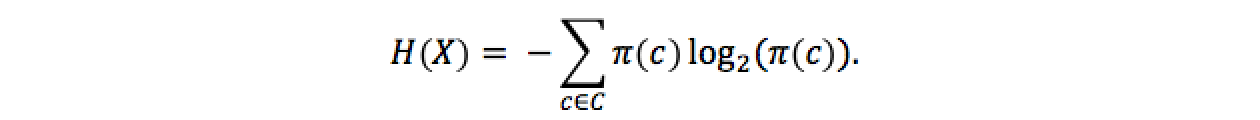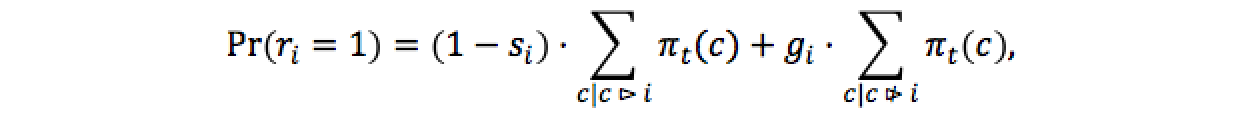Simulation et validation de tests adaptatifs dans les MOOC

Jill-Jênn VIE, Fabrice POPINEAU, Éric BRUILLARD, Yolaine BOURDA

Dans les cours en ligne, particulièrement les MOOC, la diversité des profils des apprenants et leur nombre sont tels qu'il est difficile pour un enseignant de répondre aux besoins de chacun d'entre eux. En effet, les étudiants qui se rendent sur un MOOC proviennent de différents pays, ont différents âges et parcours, et ont ainsi emmagasiné une variété de connaissances susceptible de diversifier leurs usages. Contrairement à un cours en classe, où les professeurs ont conscience des connaissances que les élèves sont censés avoir accumulées dans le passé, la pluralité des profils rend cette tâche impossible dans un MOOC.

Or, lorsqu’ils arrivent sur un MOOC, nombre de ces apprenants se posent plusieurs questions initiales : 1) Que dois-je savoir pour commencer ce cours (c'est-à-dire, est-ce que je maîtrise tous les prérequis) ? 2) Existe-t-il d'éventuelles parties du cours dont je n’ai pas besoin ? Ainsi, alors que le cours est construit de façon séquentielle, il peut arriver que certains apprenants le parcourent dans un ordre qui leur est propre (Cisel, 2016).

Afin que l'apprenant puisse répondre lui-même à ces questions initiales, le cours comprend habituellement sur la page d'inscription une section qui inclut la liste des prérequis à maîtriser afin de bénéficier de ce cours, ainsi que le programme du cours. Mais les élèves ne sont pas ceux qui sont le plus à même d'évaluer leurs connaissances (Eva et al., 2004), ainsi il serait préférable d’évaluer ces connaissances au moyen d'un test. Afin de ne pas solliciter l'apprenant avec trop de questions dès son arrivée sur le MOOC, il est préférable de poser aussi peu de questions que possible.

C'est pourquoi il nous semble particulièrement utile de proposer un diagnostic adaptatif pour éliciter les connaissances de l'apprenant, afin de déterminer et lui indiquer les composantes de connaissances qu'il connaît déjà, mais aussi celles qui lui font défaut et qu'il doit maîtriser pour pouvoir bénéficier du cours. Une fois ces lacunes identifiées, il est envisageable de les fournir à un système de recommandation intégré à la plateforme de MOOC qui proposerait à l’apprenant des ressources pour les combler.

Construire un tel diagnostic manuellement serait coûteux pour le professeur qui doit déjà préparer ses cours et les tests de validation pour obtenir le certificat. Nous préférons tirer parti du travail déjà fourni par le professeur et d’une représentation minimale du cours pour automatiser cette tâche. De plus, a priori, rien ne permet à l’enseignant d’affirmer qu’un test adaptatif réalise un diagnostic vraisemblable de l’apprenant. Nous montrons ainsi dans cet article qu'il est possible de construire des modèles de tests adaptatifs avec la simple donnée d'une représentation du cours, et de la valider à partir d’un historique de réponses à un test classique, selon une approche de crowdsourcing (Doan et al., 2011). Ainsi, une session du MOOC permet de récolter des données à partir desquelles on peut valider un diagnostic adaptatif automatique d'élicitation des connaissances, qui pourra être proposé aux apprenants s'inscrivant sur la session suivante du MOOC.

Nous commençons par exposer nos hypothèses de recherche, puis nous expliquons ce qu'est un modèle de test adaptatif ainsi que les données qu'il requiert dans notre contexte. Enfin, nous proposons une méthodologie de validation d’un modèle de test adaptatif dans un MOOC et, à titre d'exemple, nous l'appliquons aux données d'un MOOC de mathématiques de Coursera.

1.2. Hypothèses

Nous supposons que le niveau de l’apprenant n’évolue pas après qu’il a répondu à une question. Sur les plateformes de MOOC usuelles (edX, Coursera), l’apprenant ne reçoit son feedback qu’à l’issue du test, ce qui rend cette hypothèse raisonnable. Nous supposons également que les questions sont posées une par une à l’apprenant, et qu’il ne peut pas modifier ses réponses précédentes.

Nous prenons en compte le fait que l’apprenant puisse faire des erreurs d’inattention, ou deviner une bonne réponse par chance. En effet, les réponses des candidats à un test ne reflètent pas nécessairement leur maîtrise du sujet.

2. Tests adaptatifs

2.1. Principe

Les modèles de tests adaptatifs profitent du fait que les questions (aussi appelées items) sont administrées par une machine électronique (ordinateur, téléphone) afin de choisir la question suivante en fonction des réponses précédentes. Ils reposent sur deux fonctions :

Ainsi, le processus d'un test adaptatif peut se décrire de la façon simple suivante :

• Choisir la question maximisant le critère de sélection de l’item suivant ;

Les tests adaptatifs permettent de garantir une bonne mesure tout en réduisant le nombre de questions (Lan et al., 2014). Par exemple il est plus économique de ne pas poser des questions trop difficiles tant que les questions plus faciles n'ont pas été résolues, et de ne pas poser de questions dont les composantes requises semblent déjà maîtrisées. C'est en effet un moyen d'obtenir des tests plus courts et plus personnalisés, parfois même capables de faire un retour à l'apprenant sur les points à retravailler.

Cette manière d'administrer des tests n'est pas nouvelle. Les travaux sur les tests adaptatifs remontent à (Kingsbury et Weiss, 1983) et sont aujourd'hui utilisés en pratique par des tests tels que le GMAT (Graduate Management Admission Test) (Rudner, 2010) ou le GRE (Graduate Record Examination) pouvant accueillir des centaines de milliers d'étudiants (GMAC, 2013). Ils reposent sur un modèle de l'utilisateur qui permet de calibrer automatiquement le niveau des questions étant donné un historique de réponses. Ainsi, il est possible d'utiliser tout l'historique du passage du test pour poser des questions de façon adaptative. On distingue alors les tests à vocation sommative, qui ne renvoient généralement à l'apprenant qu'un score à l'issue du test, des tests à vocation formative, qui font un retour plus riche permettant à l'apprenant de s'améliorer. Ce n'est que depuis récemment (Huebner, 2010) que l'on s'intéresse à faire des tests formatifs adaptatifs, qui font un retour à l'apprenant à l'issue du test sous la forme de points maîtrisés ou non. Différents modèles de tests adaptatifs ont été proposés dans diverses communautés, ils sont comparés dans (Vie et al., 2017). Certains modèles requièrent un historique de passage pour être administrés, d’autres non.

Dans cet article, la problématique qui nous intéresse est la suivante : quels modèles de tests adaptatifs choisir dans le cadre d’un MOOC, et comment les valider empiriquement sur des données existantes ?

2.2. Tests formatifs basés sur une Q-matrice, lien entre questions et composantes de connaissance

Définie par (Tatsuoka, 1983), la q-matrice est une représentation minimale des composantes mises en œuvre dans un test. Chaque question est liée à une ou plusieurs composantes de connaissances mises en œuvre pour la résoudre. On peut donc la représenter par une matrice binaire de taille , où les questions sont en ligne, les composantes de connaissances en colonne, et l’élément de la q-matrice vaut 1 si la question fait intervenir la composante de connaissance , 0 sinon.

Il peut être fastidieux de remplir la q-matrice lorsqu'un test comporte beaucoup de questions. Certaines approches tentent de la calculer automatiquement, par exemple un algorithme de factorisation de matrices positives est utilisé par (Desmarais, 2011) pour extraire des paquets de questions qui semblent appartenir à un même groupe, afin de permettre une interprétation a posteriori. Cette méthode était déjà couramment utilisée afin d'extraire automatiquement des thèmes interprétables d'un corpus de texte, d'où sa pertinence appliquée à notre problème.

À partir d’une q-matrice, il est possible de proposer des modèles de diagnostic formatif. Par exemple, le modèle DINA (Junker et Sijtsma, 2001) consiste à ajouter à la q-matrice des paramètres d’inattention (slip) et de chance (guess) à chaque question . L’apprenant est modélisé par un état latent sous la forme d’un vecteur de bits : L’ensemble des états latents possibles C est inclus dans , le produit cartésien de K exemplaires de l’ensemble {0, 1}. Pour toute composante de connaissance k, }, si et seulement si l’apprenant maîtrise cette composante de connaissance. La probabilité qu’il réponde correctement à la question est s’il maîtrise toutes les composantes de connaissances requises par la question , spécifiées dans la q-matrice, et sinon. Ainsi, chaque observation d’une réponse de l’apprenant permet de mettre à jour une estimation de son état latent, de façon bayésienne.

Le modèle DINA a été mis en œuvre dans des tests adaptatifs (Cheng, 2009) où tout au long du test on met à jour une distribution de probabilité sur les états latents possibles dans lesquels pourrait se trouver l’apprenant au vu de ses premières réponses. Cette distribution est initialisée à la distribution uniforme : pour tout , ( désignant le cardinal de ), c’est-à-dire que tous les états latents possibles ont la même probabilité d’apparaître. Pour le modèle DINA, , le cardinal de C est donc , mais dans d’autres variantes de ce modèle que nous allons voir, peut être un sous-ensemble strict de .

Si après questions on présente la question à l’apprenant, on met à jour la distribution, selon sa réponse correcte ou incorrecte , de la façon suivante. Pour tout état latent , on a où est un coefficient de normalisation pour garantir que la somme des probabilités sur tous les états latents soit 1, et où est défini par :

Par exemple, si l’apprenant a les connaissances requises, il peut soit donner la bonne réponse en ne faisant pas d’erreur d’inattention (résultat avec probabilité ), soit faire une erreur d’inattention (résultat avec probabilité ). Cette mise à jour bayésienne permet de renforcer la masse de probabilité pour les états latents qui concordent avec les observations faites à chaque réponse de l’apprenant.

Le critère de terminaison est déclenché lorsqu’on a identifié un état latent avec probabilité supérieure à un certain seuil , par exemple 95 %, c’est-à-dire qu’il existe un tel que .

Pour choisir la question suivante, il est possible de quantifier formellement l'information que chaque question peut apporter, de façon à choisir la question la plus discriminante. En théorie de l'information, une manière de représenter l'incertitude est l'entropie. Pour une variable aléatoire pouvant prendre des valeurs avec des probabilités pour , l’entropie vaut :

Par exemple, une pièce parfaitement équilibrée peut prendre la valeur Pile avec probabilité 50 % et Face avec la même probabilité, ainsi son entropie est de 1¹, tandis qu'une autre pièce pouvant prendre la valeur Pile avec une probabilité de 90 % aura une entropie de 0,47². La pièce équilibrée est donc celle d'incertitude maximale. On notera également la valeur de . Ainsi, désigne l’incertitude du système sur l’état latent de l’apprenant après qu’il a répondu à questions. désigne l’incertitude obtenue après mise à jour, selon que l’apprenant a répondu correctement () ou non () à la question . Dans notre cas, en choisissant la question faisant le plus abaisser l'entropie en moyenne, on vise à converger rapidement vers l'état mental de l'apprenant.

Le critère de sélection de l’item suivant consiste donc à choisir la question telle que la valeur soit la plus faible. Cette quantité correspond à l’entropie moyenne après réponse de l’apprenant : connaissant la distribution à l’instant , l’apprenant a une probabilité de répondre correctement à la question égale à :

où désigne le fait que les connaissances dans l’état latent sont suffisantes pour une réponse correcte à la question et désigne le contraire. En effet, il peut répondre correctement s’il a les connaissances suffisantes et qu’il ne fait pas d’erreur d’inattention (avec probabilité ), ou s’il ne les a pas et qu’il devine la bonne réponse (avec probabilité ).

Ainsi, avec cette probabilité, l’entropie va être mise à jour en prenant en compte la réponse correcte de l’apprenant. Avec la probabilité c’est l’autre mise à jour qui sera effectuée.

Le modèle DINA a ainsi été mis en œuvre pour des tests adaptatifs, mais le nombre d’états latents possibles est , ce qui est impraticable pour de grandes valeurs de . D’autres modèles ont été proposés pour remédier à cette limitation.

2.3. Représentation minimale des connaissances par un graphe de prérequis

La théorie des espaces de connaissances (Falmagne et al., 2006) suppose que l'on a accès à une donnée du cours qui est une représentation hiérarchique des composantes de connaissance. Celle-ci est sous la forme d'un graphe où est l'ensemble des composantes de connaissance et où une arête de désigne la relation de prérequis : « la maîtrise de est un prérequis à la maîtrise de ».

Cette structure permet de réduire drastiquement le nombre d’états latents possibles () dans lesquels l’apprenant peut se trouver. Par exemple, s’il y a deux composantes de connaissance et que la relation de prérequis est , alors l’apprenant peut se trouver dans 3 états : , et . Il n’y a pas , car pour maîtriser la 2^e composante , il faut maîtriser la 1^re composante . Les critères de sélection de l’item suivant et de terminaison pour le test adaptatif sont identiques à ceux présentés dans la section précédente, c’est seulement l’ensemble des états possibles qui a changé. L’exploitation du graphe de prérequis nous a permis de diminuer le nombre d’états latents possibles jusqu’à rendre praticable la complexité d’une mise à jour après observation d’une réponse de l’apprenant.

Le modèle de hiérarchie sur les attributs (Leighton et al., 2004) permet de combiner q-matrice (dont paramètres d’inattention et de chance) et graphe de prérequis, et c’est donc celui que nous avons retenu pour notre expérience. Il est possible de calibrer les paramètres d’inattention et de chance à partir d’un historique de réponses, ou de les spécifier manuellement.

L’observation du graphe de prérequis fournit une intuition géométrique sur le fait que certaines questions sont plus informatives que d'autres. Par exemple, poser une question reliée à une composante qui n'a pas d'arc sortant mais beaucoup de nœuds prérequis est peu avantageux car la probabilité que l'étudiant la maîtrise est faible, ainsi l’apprenant a de fortes chances de ne pas y répondre correctement et cela apportera peu d’information sur son état latent.

Afin d'illustrer cette approche, nous présentons deux exemples de test adaptatif, pour lesquels on supposera que pour toute question , .

Exemple 1. Supposons que l’on ait, dans notre représentation du domaine, trois composantes de connaissance A, B, et C liées par les relations de prérequis A→B et B→C. Ainsi, l’ensemble des états possibles parmi lesquels peut se trouver l’apprenant est soit 000 (il ne maîtrise rien), soit 100 (seulement A), soit 110 (seulement A et B) soit 111 (il maîtrise tout). Il n’y a pas d’autre état latent possible, étant donné les relations de prérequis. Il y a autant de chances pour que l’apprenant se trouve dans chacun de ces cas, donc est uniforme à 0,25 et son entropie vaut 2. Supposons que nous hésitions à lui poser 3 questions, chacune faisant appel à seulement une composante de connaissance : A, B ou C. Par commodité, on appellera ces questions A, B et C. Au début du test, il y a 75 % de chances pour que l’apprenant réponde correctement à la question A (s’il est 100, 110 ou 111), 50 % de chances qu’il réponde correctement à la question B (s’il est 110 ou 111) et 25 % de chances qu’il réponde correctement à la question C (seulement s’il est 111). Ainsi, si on lui pose la question A :

- on a 75 % de chance d’observer une réponse correcte et de déduire qu’il maîtrise la composante A, et alors il ne reste plus que 3 états possibles (100, 110, 111) avec même probabilité 0,33, soit une entropie de 1,6 ;

- on a 25 % de chance d’observer une réponse incorrecte et déduire qu’il ne maîtrise rien : 000, avec probabilité 1, soit une entropie de 0.

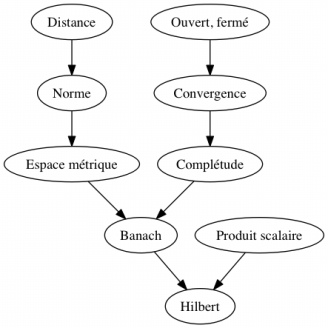
L’entropie moyenne procurée par le fait d’administrer la question A est donc . Par un raisonnement similaire et par symétrie, on aboutit à la même entropie pour la question C. En revanche, si on lui pose la question B, soit il répond correctement (50 % de chance) et on hésite alors entre 110 et 111 (entropie 1), soit il ne répond pas correctement (50 % de chance) et on hésite entre 000 et 100 (entropie 1). Donc l’entropie moyenne procurée par le fait d’administrer la question B est . Ainsi, poser la question B réduit le plus l’entropie, donc apporte plus d’information, et c’est cette question qui sera posée au début du test.

Exemple 2. Si l'on considère le graphe de prérequis de la figure 1 et que l'apprenant maîtrise toutes les notions sauf Banach et Hilbert, un test minimisant l'entropie à chaque étape et s'arrêtant lorsque l’état latent de l’apprenant a été identifié avec une probabilité de 95 % se déroulera comme suit :

À cet instant du test, la distribution de probabilité vaut 0 pour chaque état latent, sauf pour les quatre suivants qui ont la même probabilité 0,25 :

• l’apprenant maîtrise tout sauf Banach, Hilbert (il s’agit du bon état latent à identifier) ;

Alors, l'apprenant maîtrise Produit scalaire, Distance, Norme, Ouvert/fermé, Complétude, Produit scalaire, mais pas Banach, Hilbert : c’est l’état latent le plus probable étant donné les réponses qu’il a données, ainsi que le graphe de prérequis.

Ainsi, 5 questions ont été posées au lieu de 9 afin de déterminer l'état mental de l'apprenant et lui faire un retour.

3. Méthodologie de simulation et de validation d’un test adaptatif dans un MOOC

Tous les modèles de tests adaptatifs présentés précédemment sont habituellement validés sur des données simulées. Dans cet article, nous proposons une méthode automatisée pour valider des tests adaptatifs sur des données réelles issues d’un MOOC.

Un MOOC se compose habituellement de chapitres constitués de sections au terme desquelles un quiz est proposé pour que l’apprenant puisse vérifier ses connaissances. Le plus souvent, l'apprenant peut en cas d'échec repasser le quiz, de façon limitée ou illimitée.

Pour pouvoir faire un retour utile à l’apprenant, il faut considérer des modèles formatifs de test, qui s’appuient sur une q-matrice. Il faut donc spécifier le lien entre chaque question et les différentes composantes de connaissances développées dans le cours qu’elle évalue. Un test adaptatif basé sur le modèle DINA peut donc être initié.

S’il y a un grand nombre de composantes de connaissances, il faut spécifier des relations de prérequis entre les composantes de connaissances, potentiellement à l’aide du squelette du cours, afin de réduire la complexité du problème. Nous suggérons donc le modèle de hiérarchie sur les attributs dans ce cas.

3.1. Données mises en œuvre pour la validation

Afin de valider un modèle de test adaptatif formatif à partir de données réelles, nous avons besoin des éléments suivants :

- le passé des notes des utilisateurs sur la plateforme : un ensemble de motifs de réponse binaires (vrai ou faux), sous la forme où est le nombre de questions posées à tous les apprenants ;

- une représentation des composantes de connaissances mises en œuvre dans le cours ;

- la q-matrice : un lien entre chaque question et les composantes de connaissances qu'elle requiert.

- le résultat (vrai ou faux) à chaque question que le système lui a posée ;

- une estimation de la maîtrise par le candidat de chaque composante de connaissance.

3.2. Simulation et validation

Le but est de poser un minimum de questions à chaque apprenant, c’est-à-dire révéler certaines composantes de son motif de réponse de façon adaptative, et de prédire les composantes restantes du motif de réponse.

Deux métriques nous permettent de valider le modèle de test adaptatif que nous avons choisi. La première est le nombre moyen de questions avant arrêt du test (appelé temps de convergence moyen), c'est-à-dire avant que le critère de terminaison soit validé. La deuxième est le nombre de prédictions incorrectes (appelé erreur de prédiction), car il faut vérifier que le test converge vers un diagnostic qui est vraisemblable. Une fois le test terminé, à partir de l’état latent identifié, on compte le nombre de prédictions incorrectes du modèle de test adaptatif sur les questions non posées à l’apprenant pendant le test, afin d'évaluer si le diagnostic effectué par le modèle en peu de questions correspond bien aux données observées.

3.3. Ajustements

Cependant, sur un MOOC, les apprenants ne répondent pas à toutes les questions : comment considérer les entrées manquantes ? De plus, lorsque plusieurs essais sont enregistrés pour un couple apprenant/question, on peut choisir de considérer le premier ou celui de score maximum (Bergner et al., 2015). Dans notre cas, nous avons considéré à chaque fois le premier essai, pour minimiser le risque que l’apprenant devine la bonne réponse. Si l’apprenant n’a pas essayé de répondre à la question, nous comptons une réponse fausse. Dans les données des cours en ligne, on peut en effet supposer que si un apprenant a répondu à une question d’un quiz mais pas à d’autres questions issues du même quiz, c’est qu’il n’en connaît pas la réponse.

4. Mise en œuvre sur des données réelles de MOOC

Nous avons testé, sur de véritables données de MOOC issues d'un cours d'analyse fonctionnelle⁴, un modèle de test adaptatif basé sur le modèle de hiérarchie sur les attributs..

4.1. Quelques données quantitatives

Le cours a accueilli 25354 inscrits. À partir de toute la base de données SQL du MOOC, nous avons pu extraire les tests présentés dans le tableau 1.

Etape	Thème	Réponses	Questions	Remarques
Quiz 1	Topologie	5770	6	3672 étudiants
Quiz 2	Espaces métriques et normés	3296	7	2123 étudiants
Quiz 3	Espaces de Banach et fonctions linéaires continues	2467	7	1384 étudiants et une question est à réponse ouverte
Quiz 4	Espaces de Hilbert	1807	6	1101 étudiants
Quiz 5	Lemme de Lax-Milgram	1624	7	943 étudiants
Quiz 6	Espaces L_p	1504	6	831 étudiants
Quiz 7	Distributions et espaces de Sobolev	1358	9	749 étudiants
Quiz 8	Application à la simulation d’une membrane	1268	7	691 étudiants
Examen		599	10	576 étudiants

Le nombre d’étudiants – et donc de réponses aux questions – a diminué par abandon au fil du temps. Afin de simplifier l'étude tout en conservant un grand nombre de réponses, nous avons considéré le graphe de prérequis de la figure 1 et nous avons choisi un sous-ensemble de 9 questions tirées des quiz 1 à 4 du MOOC. Cela nous a permis de construire une matrice de motifs de réponse binaires de 3713⁵ étudiants sur ces 9 questions portant sur les 9 composantes de connaissance Banach, Complétude, Convergence, Distance, Espace métrique, Hilbert, Norme, Ouvert et fermé, Produit scalaire. Chaque question a été choisie pour couvrir une composante de connaissance (et toutes celles qui sont nécessaires à sa maîtrise), ainsi chaque question correspond à un nœud du graphe de prérequis. Le nombre de motifs de réponse de chaque type est donné dans le tableau 2 et sa non-uniformité laisse entendre qu'il existe des corrélations entre les réponses aux questions (sinon, le nombre d'occurrences serait le même d'un motif de réponse à un autre).

Tableau 2 • Les 30 motifs de réponse les plus fréquents pour le jeu de données extrait du MOOC d'analyse fonctionnelle

Motif	Fréquence
000000010 000000000 010110110 110111111 010110010 111111111 110111011 110110110 110110010 010010010 010110000 110111110 010010110 111111011 111110110 010110100 000110010 010100010 111110010 010010000 110111001 110011111 100010001 110111101 000010000 111011111 111110011 000010010 111111101 010100110	1129 460 271 263 122 116 77 70 42 41 40 38 37 36 35 34 27 26 21 21 21 21 20 19 18 17 16 15 15 15

4.2. Validation

Le modèle n’ayant pas besoin de données existantes pour administrer des tests adaptatifs, il n’y a pas de données d’entraînement : tous les apprenants du jeu de données sont des apprenants de test.

Pour simplifier notre analyse, nous avons initialisé tous les paramètres d’inattention et de chance à une unique valeur de robustesse , qui correspond donc à la probabilité de deviner la bonne réponse alors que la composante de connaissance correspondante n'est pas maîtrisée, ainsi qu'à la probabilité de se tromper devant une question qui requiert une composante de connaissance maîtrisée.

Pour chaque étudiant de notre jeu de données, nous simulons une interaction avec le modèle de test adaptatif qui consiste à choisir la question réduisant le plus l’incertitude (entropie) sur cet étudiant. Dès qu'on aboutit à une distribution de probabilité pour laquelle un état latent a une probabilité supérieure ou égale à 95 %, le test s'arrête. Cela permet de déterminer le nombre moyen de questions avant arrêt, ainsi que le nombre de prédictions incorrectes. Les résultats sont donnés dans le tableau 3.

Tableau 3 • Métriques principales pour la validation du modèle de test adaptatif sur les données du MOOC d'analyse fonctionnelle

Valeur de robustesse	Temps de convergence moyen	Erreur de prédiction moyenne
0	5,009 ± 0,003	1,075 ± 0,04
0,01	5,43 ± 0,016	1,086 ± 0,041
0,02	6,879 ± 0,019	1,086 ± 0,041
0,03	7,671 ± 0,027	0,956 ± 0,037
0,04	7,807 ± 0,023	1,086 ± 0,041
0,05	8,671 ± 0,027	0,956 ± 0,037

4.3. Discussion

La valeur de robustesse correspond à un test où l'on suppose que si l'apprenant répond correctement à une question, alors il maîtrise la composante de connaissance correspondante. Un tel test converge en 5 questions en moyenne, et prédit correctement 8 des 9 réponses du motif de réponse. Ainsi, en ne posant que 55 % des questions du test en fonction des réponses précédentes, il obtient un succès de 89 %.

Une plus grande valeur de robustesse donne un modèle qui requiert plus de questions pour converger car plus prudent à chaque étape dans ses déductions. Sur notre jeu de données, les prédictions ne sont pas améliorées pour autant, ce qui peut être expliqué par le faible nombre d'états possibles (35), étant donné la structure de la figure 1. Le graphe des prérequis est très rudimentaire, et n'est sans doute pas suffisant pour exprimer les connaissances d'un tel domaine des mathématiques. Toutefois, notre expérience a montré que même avec cette représentation simple du domaine évalué, le nombre de questions pouvait être réduit de moitié sans trop affecter la qualité de l’évaluation, et tout en permettant de faire un retour à l’apprenant sur ses points forts et faibles.

Pour administrer un tel test, seul le graphe de prérequis est nécessaire, il n'y a pas besoin d’avoir déjà accès à des réponses d’apprenants. En revanche, pour vérifier si un modèle de test adaptatif fonctionne, il faut avoir accès aux réponses des apprenants. De telles traces peuvent également permettre de calibrer les paramètres d’inattention et de chance (donc de robustesse) des questions, et éventuellement de déceler des erreurs d’énoncé ou des questions trop faciles, à cause des réponses proposées en QCM par exemple.

5. Conclusion et perspectives

Dans cet article, nous avons fait un état de l’art des modèles de tests adaptatifs et présenté une méthode pour les valider sur des données réelles. Nous l’avons mise en œuvre sur des données réelles issues d’un MOOC pour montrer que le modèle de hiérarchie sur les attributs (Leighton et al., 2004) peut réduire le nombre de questions posées tout en garantissant la fiabilité du test.

Ce modèle se distingue de ceux utilisés en psychométrie, tels que le modèle de Rasch, car il ne nécessite pas de données existantes pour fonctionner et permet de faire un retour à l'étudiant sur les points non maîtrisés. À la fin du test, il est ainsi possible d’indiquer à l’apprenant : « Voici les prérequis qui semblent vous faire défaut », et éventuellement le rediriger vers des contenus qui peuvent l’aider à y remédier. Le fait de nommer ce que l’apprenant ne sait pas lui permet de pouvoir choisir comment acquérir ses connaissances, sur le cours ou par d’autres moyens. Il est également possible d’identifier les points forts des apprenants et de leur permettre de sauter d’éventuelles parties du cours consistant en des rappels.

Afin d’étendre la recherche présentée dans cet article, il faudrait étudier le nombre de questions nécessaires à l’arrêt du test, ainsi que la pertinence du diagnostic obtenu en fonction de différentes valeurs du seuil pour le critère de terminaison (ici, nous n’avons considéré que 95 %). C’est l’objet de nos travaux futurs.

Nous avons montré comment un modèle simple tel que celui de hiérarchie sur les attributs où tous les paramètres d’inattention et de chance sont rassemblés en un unique paramètre de robustesse permettait déjà de réduire le nombre de questions de façon satisfaisante. Pour aller plus loin, il faudrait essayer de calibrer automatiquement les paramètres d’inattention et de chance à partir d’une partie de la population de l’historique afin de voir si le modèle résiste davantage aux erreurs des apprenants.

Dans certains domaines moins procéduraux que les mathématiques, comme les langues, le graphe de prérequis peut être difficile à construire. Il serait bon de pouvoir, à partir des données des apprenants, suggérer des modifications du graphe. Un modèle de diagnostic de connaissances permettant d’exprimer le fait qu’une composante de connaissances puisse intervenir plus ou moins dans la résolution d’une question est présenté dans (Vie et al., 2016).

La représentation des composantes de connaissances à diagnostiquer sous la forme d'un graphe de prérequis peut être vue comme une ontologie minimale. D'autres modèles de tests non adaptatifs considèrent des ontologies pour la représentation des connaissances, tels que (Mandin et Guin, 2014). Des variantes adaptatives pourraient être développées pour réduire le nombre de questions, et de tels modèles permettraient d’enrichir le diagnostic rendu à l’apprenant à l’issue du test.

Remerciements

Nous remercions John Cagnol de nous avoir communiqué la base de données de son cours sur la plateforme Coursera et Benoît Choffin pour ses commentaires. Ce travail est soutenu par l'Institut de la Société Numérique de Paris-Saclay, financé par l'IDEX Paris-Saclay, ANR-11-IDEX-0003-02.

À propos des auteurs

Jill-Jênn Vie est chercheur postdoctoral en apprentissage automatique (machine learning) dans l’équipe Human Computation du laboratoire RIKEN AIP de Tokyo. Sa recherche porte sur l’interaction avec des systèmes d’apprentissage automatique (active learning) et sur la prise de décision avec des données incertaines (crowdsourcing). Il a effectué sa thèse sur les tests adaptatifs avec Fabrice Popineau, Yolaine Bourda et Éric Bruillard. Ses travaux s’appliquent à l’analytique de l’apprentissage (learning analytics, comment utiliser les traces d’apprenants pour améliorer l’apprentissage) et aux systèmes de recommandation. Il est consultant pour le projet PIX de certification des compétences numériques lancé par le ministère de l’Éducation, et contribue au code libre de la plateforme.

Adresse : RIKEN AIP – Nihonbashi 1-4-1 – Mitsui Building 15F – Chuo-ku, Tokyo 103-0027, Japan

Fabrice Popineau est professeur en informatique à CentraleSupélec et chercheur permanent au Laboratoire de Recherche en Informatique (UMR8623 de l’Université Paris-Saclay et du CNRS). Ses recherches portent depuis une quinzaine d’années sur les apports de l’intelligence artificielle aux plateformes éducatives en ligne. Il s’intéresse en particulier à divers aspects de la personnalisation : que peut apporter l’analytique de l’apprentissage en termes de construction de profil ? Comment recommander efficacement des ressources pédagogiques individuellement ? Comment accompagner l’apprenant et remédier à ses difficultés ?

Adresse : CentraleSupélec/LRI – Université Paris-Saclay – Bât 650 Ada Lovelace – rue Noetzlin, 91190 Gif-sur-Yvette

Éric Bruillard est professeur des universités au laboratoire EDA, université Paris Descartes Ses recherches portent, depuis plus d'une trentaine d'années, sur les questions de conception et d'usage des technologies issues de l'informatique dans l'éducation. Elles ont été menées d'abord avec le Centre mondial de l'informatique (années 80), puis en relation avec l'INRP (institut national de recherche pédagogique) avec le département TECNE, au LIUM (laboratoire d'informatique de l'université du Maine) et au Greyc (équipe IsLand), puis au sein de l'UMR STEF (ENS Cachan). Elles s'inscrivent à l'articulation entre l'informatique, les sciences de l'éducation et les sciences de l'information et de la communication. Elles couvrent des questions de didactique de l'informatique, de didactique des progiciels et de formation des enseignants aux technologies issues de l'informatique, de Mooc et d’usages des ressources éducatives.

Adresse : Laboratoire EDA, Université Paris Descartes, 45 rue des Saints-Pères, 75270 Paris cedex 06

Yolaine BOURDA est professeure d’informatique et directrice du département informatique de CentraleSupélec. Elle est chercheuse au Laboratoire de Recherche en Informatique (UMR 8623). Ses recherches portent sur les Environnements Informatiques pour l’Apprentissage Humain (EIAH) et plus particulièrement sur leur personnalisation. Elle est aussi experte auprès du comité de normalisation ISO/IEC JTC1/SC36 « Technologies de l’Information pour l'apprentissage, l'éducation et la formation ».

REFERENCES

Bergner, Y., Colvin, K. et Pritchard, D. E. (2015). Estimation of ability from homework items when there are missing and/or multiple attempts. Dans Proceedings of the fifth international conference on learning analytics and knowledge (LAK 2015) (p. 118–125). ACM.

Cheng, Y. (2009). When cognitive diagnosis meets computerized adaptive testing: CD-CAT. Psychometrika, 74(4), 619–632.

Cisel, M. (2016). Utilisations des MOOC : éléments de typologie. Retour sur la diversité des formes d’attrition (Thèse de doctorat, ENS Paris-Saclay). Disponible sur internet.

Desmarais, M. C. (2011). Conditions for effectively deriving a q-matrix from data with non-negative matrix factorization. Dans Proceedings of the 4th international conference on educational data mining (EDM 2011) (p. 41–50).

Desmarais, M. C. et Baker, R. S. (2012). A review of recent advances in learner and skill modeling in intelligent learning environments. User Modeling and User-Adapted Interaction, 22(1-2), 9–38.

Doan, A., Ramakrishnan, R. et Halevy, A. Y. (2011). Crowdsourcing systems on the world-wide web. Communications of the ACM, 54(4), 86–96.

Eva, K. W., Cunnington, J. P., Reiter, H. I., Keane, D. R. et Norman, G. R. (2004). How can i know what i don’t know? Poor self-assessment in a well-defined domain. Advances in Health Sciences Education, 9(3), 211–224.

Falmagne, J.-C., Cosyn, E., Doignon, J.-P. et Thiéry, N. (2006). The assessment of knowledge, in theory and in practice. Dans R. Missaoui et J. Schmidt (dir.), Formal concept analysis (p. 61–79). Berlin, Allemagne : Springer.

Huebner, A. (2010). An overview of recent developments in cognitive diagnostic computer adaptive assessments. Practical Assessment, Research et Evaluation, 15(3). Disponible sur internet.

Junker, B. W. et Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258-272.

Kickmeier-Rust, M. D. et Albert, D. (2016). Competence-based knowledge space theory. Dans P. Reimann et al. (dir.), Measuring and Visualizing Learning in the Information-Rich Classroom, 109—120. Routledge.

Kingsbury, G. et Weiss, D. (1983). New horizons in testing: Latent trait test theory and computerized adaptive testing. New York, NY : Academic Press.

Lan, A. S., Waters, A. E., Studer, C. et Baraniuk, R. G. (2014). Sparse factor analysis for learning and content analytics. The Journal of Machine Learning Research, 15(1), 1959-2008.

Leighton, J. P., Gierl, M. J. et Hunka, S. M. (2004). The attribute hierarchy method for cognitive assessment: a variation on tatsuoka’s rule-space approach. Journal of Educational Measurement, 41(3), 205–237.

Lynch, D. et Howlin, C. P. (2014). Real world usage of an adaptive testing algorithm to uncover latent knowledge. Dans Proceedings of the 7th International Conference of Education, Research and Innovation (ICERI 2014) (p. 504-511). IATED.

Mandin, S. et Guin, N. (2014). Basing learner modelling on an ontology of knowledge and skills. Dans Proceedings of 14th international conference on Advanced learning technologies (ICALT 2014) (p. 321–323). IEEE.

Rudner, L. M. (2010). Implementing the graduate management admission test computerized adaptive test. Dans W. J. van der Linden, C. A.W. Glas (dir.), Elements of adaptive testing (p. 151–165). Springer Nature.

Tatsuoka, K. K. (1983). Rule space: an approach for dealing with misconceptions based on item response theory. Journal of Educational Measurement, 20(4), 345–354.

Vie, J.-J., Popineau, F., Bourda, Y. et Bruillard, É. (2016). Adaptive testing using a general diagnostic model. Dans European conference on technology enhanced learning (EC-TEL 2016) (p. 331–339). Springer.

Vie, J.-J., Popineau, F., Bourda, Y. et Bruillard, É. (2017). A review of recent advances in adaptive assessment. Dans A. Pena-Ayala (dir.), Learning analytics: fundaments, applications, and trends: a view of the current state of the art to enhance e-learning. Berlin, Allemagne : Springer.

³ Il s’agira d’une question permettant d’évaluer si l’apprenant maîtrise la composante de connaissance « Produit scalaire » ou non. Idem pour les questions suivantes.

⁴ Ce cours a été donné par John Cagnol, professeur à CentraleSupélec, sur la plateforme Coursera en 2014.

⁵ Certains étudiants ont répondu au second quiz sans avoir répondu au premier. Il n’y a pas d’inclusion stricte à ce niveau.