 Sciences et Technologies
Sciences et Technologies de l´Information et
de la Communication pour
l´Éducation et la Formation
Volume 14, 2007
Article de recherche

Analyse et représentation en deux dimensions de traces pour le suivi de l'apprenant
Nicolas DELESTRE, Nicolas
MALANDAIN ![]() LITIS,
INSA de Rouen
LITIS,
INSA de Rouen![]()
![]() RÉSUMÉ : Le
suivi d'apprenants lors de la résolution de problèmes est
difficile, surtout lorsque le nombre d'apprenants est important ou lorsque la
résolution de problèmes se fait à distance. Nous proposons
ici une représentation graphique en deux dimensions des traces de ces
apprenants qui pourrait être utilisée dans un logiciel de
« monitoring ». Pour arriver à ce résultat
nous avons adapté et combiné des algorithmes d'analyse
numérique (principalement des algorithmes de réduction de
dimensions : carte de Kohonen et SNE). Nous avons aussi abordé la
problématique de distance entre ensembles en proposant une nouvelle
mesure de similarité lorsque leurs éléments sont
sémantiquement proches. Enfin nous avons validé et
amélioré notre approche à l'aide tout d'abord de
données simulées, puis de données réelles issues
d'une expérimentation.
RÉSUMÉ : Le
suivi d'apprenants lors de la résolution de problèmes est
difficile, surtout lorsque le nombre d'apprenants est important ou lorsque la
résolution de problèmes se fait à distance. Nous proposons
ici une représentation graphique en deux dimensions des traces de ces
apprenants qui pourrait être utilisée dans un logiciel de
« monitoring ». Pour arriver à ce résultat
nous avons adapté et combiné des algorithmes d'analyse
numérique (principalement des algorithmes de réduction de
dimensions : carte de Kohonen et SNE). Nous avons aussi abordé la
problématique de distance entre ensembles en proposant une nouvelle
mesure de similarité lorsque leurs éléments sont
sémantiquement proches. Enfin nous avons validé et
amélioré notre approche à l'aide tout d'abord de
données simulées, puis de données réelles issues
d'une expérimentation.
![]() MOTS CLÉS : Visualisation
de traces, projection 2D de données symboliques,
distance/similarité entre ensembles, cartes conceptuelles, carte de
Kohonen, algorithme du SNE.
MOTS CLÉS : Visualisation
de traces, projection 2D de données symboliques,
distance/similarité entre ensembles, cartes conceptuelles, carte de
Kohonen, algorithme du SNE.
![]() ABSTRACT : The
learner follow-up in problem solving is a hard issue. It is more difficult when
there are a lot of learners or when those learners use distance learning. We
propose in this paper a two-dimensional graphic representation of student's
traces. To achieve this goal, we use and modify numerical analysis algorithms
(automatic dimensionality reduction algorithms like Self Organizing Map and
Stochastic Neighbour Embedding). We also propose a new distance between sets
whose elements have semantic similarity. Finally, we validate and improve our
algorithm with simulated data and experimental data.
ABSTRACT : The
learner follow-up in problem solving is a hard issue. It is more difficult when
there are a lot of learners or when those learners use distance learning. We
propose in this paper a two-dimensional graphic representation of student's
traces. To achieve this goal, we use and modify numerical analysis algorithms
(automatic dimensionality reduction algorithms like Self Organizing Map and
Stochastic Neighbour Embedding). We also propose a new distance between sets
whose elements have semantic similarity. Finally, we validate and improve our
algorithm with simulated data and experimental data.
![]() KEYWORDS : Display
of student traces, symbolic data 2D projection, conceptual maps, distance
between sets, Self Organizing Maps, Stochastic Neighbour Embedding algorithm
KEYWORDS : Display
of student traces, symbolic data 2D projection, conceptual maps, distance
between sets, Self Organizing Maps, Stochastic Neighbour Embedding algorithm
3. Les traces pour le suivi de l'apprenant
4. Comment projeter des informations sur un plan ?
6. Amélioration en prenant en compte la similarité entre attributs
1. Introduction
Lorsqu'un enseignant encadre des travaux pratiques, son objectif est d'évaluer les apprenants pour détecter au plus tôt ceux qui rencontrent des problèmes. Les moyens mis à sa disposition varient suivant le domaine d'application. Par exemple en laboratoire de langue, l'enseignant dispose d'un pupitre lui permettant de choisir l'étudiant qu'il va écouter. En informatique, l'enseignant passe d'apprenant en apprenant et observe leur production sur l'écran. Pour optimiser son temps, il pourra, s'il connaît déjà les apprenants et donc leur niveau, passer plus de temps avec ceux qui vont être a priori en difficulté. Le problème est que cet encadrement n'est plus réalisable lorsque le nombre d'apprenants augmente, ou lorsque l'enseignement est dispensé à distance.
C'est à partir de ce constat que avons travaillé sur la création d'indicateurs permettant d'alerter l'enseignant si besoin est. Mais de quelles informations disposons-nous ? En fait, seules les actions de l'apprenant sont accessibles, c'est ce que l'on nomme les traces.
Parallèlement, depuis maintenant quelques années nous utilisons un ensemble d'outils développés par F. Delorme (Delorme, 2005) permettant d'évaluer les apprenants. Nous leur demandons de construire des cartes conceptuelles. Ces cartes sont ensuite analysées et un des outils permet de les positionner sur un plan, et donc d'identifier celles qui sont proches ou éloignées des solutions.
En s'inspirant de ces résultats nous avons eu l'idée de représenter dynamiquement les traces des apprenants sur un plan afin de former des chemins. Ceci permettra à l'enseignant de savoir rapidement si l'apprenant tend ou non vers la bonne solution.
Après avoir rappelé les concepts importants de notre environnement d'évaluation, nous étudierons l'utilisation de traces explicites de l'apprenant afin de caractériser son avancement dans la résolution d'un problème. Puis nous proposerons une restitution synthétique de cette information à l'enseignant afin qu'il puisse se faire un avis sur l'apprenant.
L'analyse automatique des traces ainsi que la restitution de l'information nous amèneront à des problèmes de classification, l'apprenant est-il ou non dans la bonne direction ? Puis nous présenterons des algorithmes de réduction de dimensions (SNE, cartes de Kohonen) qui permettront de projeter des informations sur un plan afin de visualiser « l'état » de l'apprenant.
Nous présenterons l'originalité de notre approche qui utilise un algorithme de projection basé sur l'utilisation conjointe du SNE et des cartes de Kohonen dont la phase d'apprentissage a été adaptée à notre problématique. Puis nous proposerons une amélioration basée sur une dissimilarité ensembliste pondérée par une mesure de similarité entre les éléments de ces ensembles.
Nous conclurons alors sur une validation expérimentale de nos travaux où nous montrerons que nous arrivons à caractériser les apprenants effectuant des exercices.
Mais nous commencerons par présenter le contexte dans lequel nous travaillons, c'est-à-dire notre environnement d'évaluation et l'ensemble des outils qui le composent.
2. Contexte
Le contexte de ce travail s'inscrit dans les travaux de thèse de Fabien Delorme (Delorme, 2005) sur l'évaluation des apprenants concernant les deux premiers niveaux de connaissances de la taxonomie de Bloom (Bloom, 1956) : les niveaux « connaissance » et « compréhension ». F. Delorme a constaté qu'il n'existe pas de logiciel d'évaluation qui minimise les trois contraintes suivantes :
- donner assez de liberté à l'apprenant pour qu'il puisse exprimer ce qu'il sait,
- minimiser le travail en amont de l'évaluation, c'est-à-dire ne pas fournir trop de connaissance au système pour effectuer l'évaluation,
- minimiser le travail de l'enseignant en aval de l'évaluation, c'est-à-dire obtenir une évaluation (semi-)automatique.
Par exemple les QCM, qui permettent d'obtenir une correction automatique, minimisent bien le troisième critère, mais laissent peu d'initiative à l'apprenant et demandent à l'enseignant un travail important de préparation comme l'indique J-M. Labat (Labat, 2002).
En s'inspirant des travaux en science de l'éducation de Britt-Mari Barth (Bart, 1993), F. Delorme a proposé une méthode et des outils pour l'évaluation des apprenants en utilisant les cartes conceptuelles. L'objectif est de demander à l'apprenant d'expliciter des notions (concepts à définir) en les reliant à d'autres concepts. Le couple relation/concept cible pour une notion est nommé « attribut ».
Par exemple, la carte de la figure 1 décrit la notion « Objet Stub » en lui associant les quatre attributs :
- « est une instance », « classe Stub »,
- « se trouve dans/sur », « client RMI »,
- « envoie des requêtes », « objet skeleton »,
- « reçoit des résultats », « objet skeleton ».
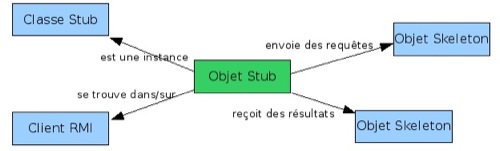
Figure 1 • Une carte conceptuelle définissant la notion Objet Stub
Ce type de carte permet d'évaluer le premier niveau de la taxonomie de Bloom, le niveau connaissance. Mais lorsque l'on demande aux apprenants de définir plusieurs notions d'un cours, un concept cible pour une notion donnée peut aussi être une notion à définir. Dès lors l'apprenant est obligé d'exprimer les relations qu'il y a entre les notions d'un cours, d'où une évaluation du niveau compréhension. Par exemple, la figure 2 présente les notions du cours sur la technologie Java RMI : en vert les notions du cours (« Class Stub », « Client RMI », « Objet distribué RMI », etc.) et en bleu les concepts (« Interface serializable », « Interface Remote », etc.).
F. Delorme (Delorme, 2005) a montré que la correction manuelle de cartes conceptuelles donnait des résultats équivalents à la correction des définitions des mêmes notions en langue naturelle. Il a de plus montré que des algorithmes de classification (k-ppv, (Cover et Hart, 1967) et carte de Kohonen, (Kohonen, 2001)) pouvaient donner des résultats proches d'une classification manuelle. En contrepartie, l'utilisation de ces algorithmes oblige l'enseignant à lister l'ensemble des concepts et des relations utilisables pour définir une notion. De plus ces concepts et ces relations doivent être organisés hiérarchiquement (par l'enseignant) suivant la relation « est un » à l'image des supports dans les graphes conceptuels (Genest, 2002). La figure 3 propose une partie du support qui a permis de créer la carte précédente.
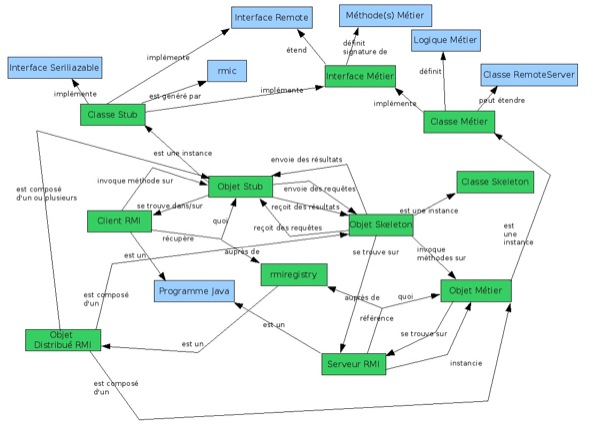
Figure 2 • Union de cartes conceptuelles présentant les notions liées à RMI
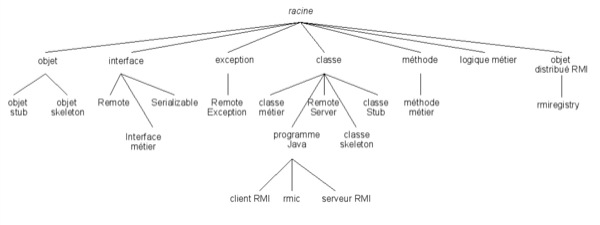
Figure 3 • Hiérarchie des concepts pour définir les notions du cours RMI
Pour valider l'hypothèse que la production de cartes conceptuelles par l'étudiant est évaluable automatiquement, F. Delorme a développé plusieurs logiciels :
- Diogen, l'éditeur de cartes conceptuelles (Cf. figure 4),
- Monime, l'évaluateur de cartes conceptuelles utilisant l'algorithme des k-ppv,
- Anthystène, le logiciel permettant de classer des cartes et obtenir un rendu graphique de cette classification. Il utilise l'algorithme des cartes de Kohonen que nous allons détailler par la suite.
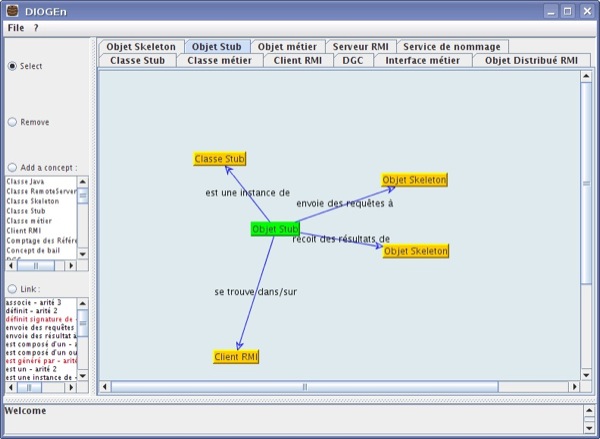
Figure 4 • Interface utilisateur du logiciel Diogen
Cette méthode et ces outils ont été utilisés à plusieurs occasions dans le cadre de deux cours d'informatique : un cours d'algorithmique sur les tris et un cours d'informatique répartie sur la technologie Java RMI (JDK 1.3). C'est lors d'une de ces dernières expérimentations que nous avons enregistré les actions des apprenants qui ont servi de données au travail présenté dans cet article.
3. Les traces pour le suivi de l'apprenant
Comme nous venons de le voir, notre environnement d'évaluation propose différents outils pour situer l'apprenant en termes de résultat. L'enseignant, qui utilise ces outils n'est pas dans la même situation qu'une correction de copie. Il ne voit que le résultat final et aucunement la méthode avec laquelle l'apprenant a atteint son but ou pas. Nous souhaitons donc proposer à l'enseignant un outil permettant de suivre un à un les apprenants afin de voir comment ils avancent et si possible les guider vers « la solution ».
3.1. La dynamique du couple apprenant/enseignant
Nous avons d'une part l'apprenant qui utilise Diogen pour résoudre un exercice (c.-à-d. construire des cartes conceptuelles). Il effectue donc des actions explicites telles que des ajouts/retraits de concepts, de relations, ... mais aussi des actions implicites (comme les mouvements de souris ou encore son comportement devant la machine). D'autre part, nous avons l'enseignant qui souhaite cibler un apprenant pour voir comment il travaille. Dans le cas d'un cours en présentiel (ou par « vidéo interposée ») l'enseignant pourrait utiliser son expérience et détecter en partie les comportements d'apprenants en difficulté. Dans le cas d'un suivi à distance les seuls retours possibles pour l'enseignant seront les actions « informatiques » de l'apprenant et l'état d'avancement de l'exercice.
L'enseignant à distance ne peut pas se permettre d'analyser en parallèle tous les apprenants effectuant l'exercice. C'est pourquoi nous devons lui fournir un outil analysant automatiquement les actions des apprenants et l'état des exercices pour l'aiguiller vers les apprenants en difficulté. Nous devons tout d'abord choisir les actions à analyser. Les actions explicites sont très intéressantes puisqu'elles influent directement sur l'état de l'exercice. En ce qui concerne les actions implicites, comme le comportement de l'apprenant, il est plus difficile de les modéliser et de les analyser sans faire appel aux sciences du comportement. De la même façon les mouvements de souris dépendent énormément du sujet (rapidité, dextérité, ...) et font plus appel à une étude du sujet humain que nous ne sommes pas pour l'instant en mesure d'effectuer.
Dans le cadre de nos travaux nous nous sommes penchés sur les données les plus objectives et les plus « facilement récupérables », c'est-à-dire les actions explicites (ajout/retrait de concepts/relations). Il est alors possible, à partir de ces informations, de reconstituer tout le cheminement daté de l'apprenant par rapport à sa situation actuelle de résolution de l'exercice. Grâce à ces traces, l'enseignant pourrait être en mesure d'évaluer la démarche de l'apprenant, savoir où il se situe et si il est en difficulté ou non. Le problème est que ces traces brutes demandent un temps d'analyse humain trop important pour porter l'attention sur toute une classe.
3.2. Analyse et restitution de l'information
L'analyse automatique des traces est donc indispensable pour aider l'enseignant dans son ciblage des apprenants. Non seulement l'enseignant doit rapidement voir quel apprenant est en difficulté, mais aussi où se situe la difficulté.
L'analyse faite par la machine doit être restituée de manière synthétique afin de permettre une lecture rapide. Une des façons les plus simples pour synthétiser l'information serait d'utiliser la métaphore du feu tricolore pour chaque apprenant. Le feu rouge, l'apprenant est en grande difficulté, le feu vert l'apprenant n'a pas de problème et enfin le feu orange l'apprenant s'égare. Cette métaphore est séduisante de prime abord puisque l'enseignant saurait rapidement détecter les apprenants problématiques. C'est d'ailleurs ce que proposent R. Mazza et V. Dimitrova dans (Mazza et Dimitrova, 2007) en associant une couleur aux couples (exercice, étudiant). L'enseignant dispose d'une vue synthétique contenant l'ensemble des étudiants et des exercices ainsi que le niveau de réussite indiqué par une couleur.
L'objectif de nos travaux vise a caractériser de manière plus précise la progression de l’apprenant lors de la résolution d’un exercice. Nous allons pour cela introduire une notion de similarité (distance) entre ce que propose l'apprenant et des solutions.
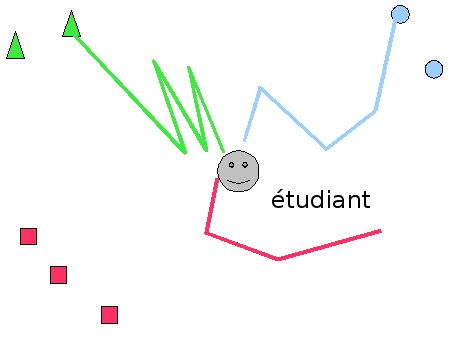
Figure 5 • Proposition de représentation de traces
Dans la figure 5, nous proposons une représentation de l'analyse automatique des traces susceptible d'être exploitable par un enseignant. La figure représente sur un plan trois exercices (triangle, rond, carré) ayant chacun plusieurs solutions (2 pour triangle et rond, 3 pour carré). L'apprenant est placé au centre de la carte. Les tracés représentent la distance à laquelle l'apprenant se trouve des solutions. Le tracé bleu (qui mène aux ronds) montre que l'apprenant trouve assez rapidement la solution. Le tracé vert (qui mène aux triangles) montre que l'apprenant atteint une solution mais a fait preuve d'hésitations (allers-retours). Enfin le tracé rouge montre que l'apprenant s'éloigne de la solution.
La représentation en deux dimensions que nous proposons ici, nous confronte à deux problèmes. D'une part, comment modéliser les traces afin d'y associer la notion de distance. D'autre part comment projeter ces informations dans un espace à deux dimensions.
4. Comment projeter des informations sur un plan ?
4.1. Algorithmes de projection de données de 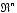
Dans le domaine de l'analyse numérique, les
algorithmes qui transforment des données de ![]() , nommés
dans ce cas « points », en données de
, nommés
dans ce cas « points », en données de ![]() avec m<n
sont appelés algorithmes de réduction de dimension. La
difficulté consiste à conserver certaines caractéristiques
des données initiales : des points proches dans
avec m<n
sont appelés algorithmes de réduction de dimension. La
difficulté consiste à conserver certaines caractéristiques
des données initiales : des points proches dans ![]() doivent avoir des
images (nommées projections) proches dans
doivent avoir des
images (nommées projections) proches dans ![]() . Inversement, des
points éloignés dans
. Inversement, des
points éloignés dans ![]() doivent avoir des
projections éloignées. On dit aussi que les projections de
données similaires (ou dissimilaires) donnent des données
similaires (respectivement dissimilaires).
doivent avoir des
projections éloignées. On dit aussi que les projections de
données similaires (ou dissimilaires) donnent des données
similaires (respectivement dissimilaires).
La méthode la plus ancienne, et aussi la plus connue, qui permet cette transformation est l'Analyse en Composantes Principales (Hotelling, 1933) et (Lebart et al, 1982). Cependant, l'un des inconvénients de cette méthode est qu'elle ne conserve la dissimilarité entre les données que si ces dernières ont certaines caractéristiques (elles doivent être linéaires). Pour pallier ce problème, depuis quelques années, plusieurs autres méthodes ont été proposées, comme par exemple le Local Linear Embbeding (Roweis et Saul, 2000). L. van der Maaten (van der Maaten, 2007) propose une liste, à notre connaissance, exhaustive de ce type d'algorithmes avec la possibilité de télécharger leurs implantations en matlab ainsi que des exemples de jeux de tests.
Parmi ces nombreuses méthodes, deux d'entre elles nous ont particulièrement intéressés. La première est l'algorithme du SNE (Stochastic Neighbor Embedding (Hinton et Roweis, 2003)) pour la qualité de ses projections. La seconde est basée sur l'utilisation des cartes de Kohonen (ou cartes auto-organisatrices, ou SOM pour Self Organizing Map (Kohonen, 2001) pour ses possibilités de généralisation. Étudions plus en détail ces deux méthodes.
4.1.1. SNE
L'algorithme du SNE est assez simple dans son principe. Nous avons des données dans un espace de départ et leurs projections dans l'espace d'arrivée (ces dernières sont positionnées initialement aléatoirement). L'objectif est de « déplacer » ces projections afin de faire correspondre les distances entre les données et celles entre les projections. Pour simplifier, cet algorithme suit les trois étapes suivantes :
- Déterminer aléatoirement des coordonnées des projections;
- Calculer les deux « matrices des distances » entre éléments (p matrice des distances dans l'espace de départ, q celle dans l'espace d'arrivée);
- Minimiser la différence entre ces deux matrices en déplaçant les projections.
Plus formellement, soit xi les données à projeter et yi leurs projections. On nomme pij la distribution de probabilité telle que xi ait pour voisin xj.
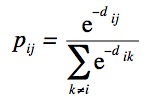
avec dij la distance euclidienne entre xi et xj.
De la même manière, on nomme qij la distribution de probabilité telle que yi ait pour voisin yj.
Soit le coût C défini comme étant la somme des
distances de Kullback-Leibler entre pij et
qij (![]() ).Comme nous le
disions, l'objectif de cet algorithme est de
« déplacer » les yi, et donc de
modifier qij, afin de minimiser le coût C.
).Comme nous le
disions, l'objectif de cet algorithme est de
« déplacer » les yi, et donc de
modifier qij, afin de minimiser le coût C.
Au début de l'algorithme, les yi sont
positionnés au hasard autour de l'origine dans l'espace d'arrivée.
Par la suite, on minimise le coût C à l'aide d'un algorithme
de descente de gradient. Cet algorithme itératif déplace les
yi jusqu'à ce que C soit plus petit qu'une
valeur ![]() donnée. Les
yi sont déplacés de la façon suivante
:
donnée. Les
yi sont déplacés de la façon suivante
:
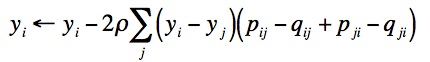
où ![]() est le pas
d'itération (au départ à 1 et qui peut diminuer [
est le pas
d'itération (au départ à 1 et qui peut diminuer [![]() ] dans le cas
où
] dans le cas
où ![]() ).
).
L'avantage de cet algorithme est la qualité de la projection. Par
exemple la figure 6 montre comment sont projetés dans ![]() des points de
des points de
![]() caractérisant des chiffres manuscrits représentés à
l'aide de matrices 16x16 de pixels gris.
caractérisant des chiffres manuscrits représentés à
l'aide de matrices 16x16 de pixels gris.
Toutefois l'algorithme du SNE a un grand inconvénient, il ne permet pas de généraliser une projection : l'ajout d'un nouveau x demandera de tout recalculer.
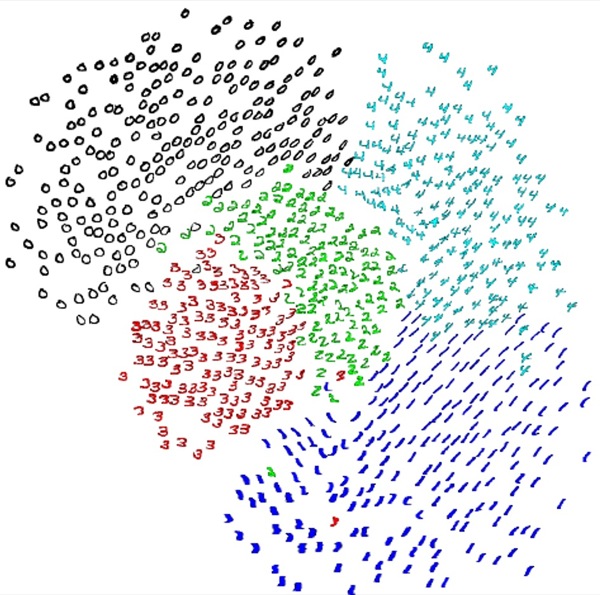
Figure 6 • Projection dans ![]() de points de
de points de
![]() représentant des chiffres manuscrits (issu de
(Hinton et Roweis, 2003))
représentant des chiffres manuscrits (issu de
(Hinton et Roweis, 2003))
4.1.2. Carte de Kohonen
Une carte de Kohonen est un réseau de neurones non supervisé (on n'étiquette pas les données qui vont servir à la phase d'apprentissage). Sa topologie est souvent un quadrillage (pour une projection 2D), où chaque neurone est connecté à quatre de ses voisins. À chaque neurone est associé un élément de l'espace de départ (choisi initialement aléatoirement) que l'on nomme « prototype ».
Comme pour tout réseau de neurones, on ne peut utiliser une carte de Kohonen qu'après lui avoir présenté les données qui la paramètrent : c'est la phase d'apprentissage. Dans le cas des cartes de Kohonen, l'objectif de cette phase est de « déplacer » certains prototypes vers les données d'apprentissage. Pour ce faire, on présente successivement ces données à tous les neurones qui composent la carte de Kohonen. Celui dont le prototype est le plus proche de la donnée présentée est nommé « neurone gagnant » (et son prototype, le « prototype gagnant »). À partir de ce neurone gagnant, on sélectionne un ensemble de neurones faisant partie de son « voisinage ». On rapproche linéairement les prototypes des neurones de ce voisinage ainsi que le prototype gagnant vers la donnée d'apprentissage. Finalement, on réitère ces actions jusqu'à ce que les déplacements des prototypes soient « faibles ».
Ceci peut être formalisé par l'algorithme de la figure 7 (inspiré de l'algorithme proposé par P. Preux (Preux, 2007)).

Figure 7 • Phase d'apprentissage d'une carte de Kohonen
Il est à noter que la taille du voisinage du prototype gagnant (qui détermine les prototypes p candidats au rapprochement) est fonction de l'itération (plus on avance dans la phase d'apprentissage plus la taille du voisinage se réduit). De la même manière, la vitesse de rapprochement v des prototypes du voisinage et du neurone gagnant est fonction de l'itération (plus on avance dans l'itération moins la vitesse est grande) et du prototype gagnant (plus p est éloigné de g plus la vitesse est faible).
Après la phase d'apprentissage, nous pouvons utiliser les cartes de Kohonen pour projeter une donnée d de l'espace de départ. L'algorithme sélectionne le neurone gagnant, c'est-à-dire le neurone dont le prototype est le plus proche de d. Les cartes de Kohonen sont intéressantes pour leur qualité de projection mais surtout pour leurs performances en généralisation. Par exemple la figure 8 représente, à l'aide de couleurs, les prototypes d'une carte de Kohonen de 100x100 neurones à l'issue d'une phase d'apprentissage. Les données d'apprentissage utilisées (éléments de [0..255]3) étaient uniquement les couleurs blanche, rouge, verte, bleue et jaune. On constate que des couleurs intermédiaires entre ces cinq couleurs sont automatiquement prises en compte comme l'indiquent les flèches sur la figure.
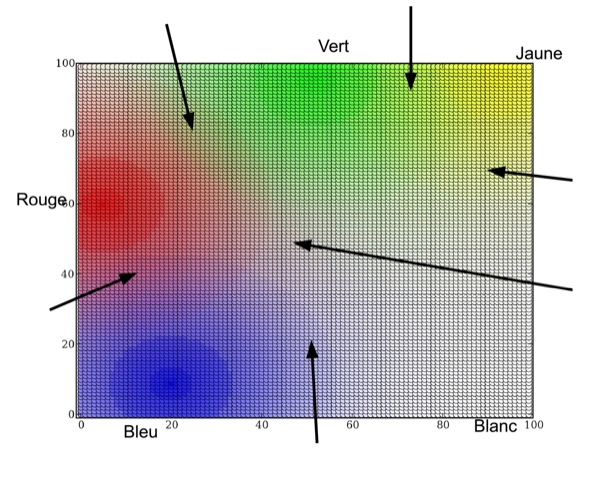
Figure 8 • Visualisation des prototypes ([0..255]3) d'une carte de Kohonen à l'issue de l'apprentissage de 5 couleurs
4.2. Application aux données ensemblistes
Une des caractéristiques de ces deux algorithmes est de faire peu de prérequis sur les données initiales : seule une mesure de similarité, ou mieux une distance, entre deux éléments est obligatoire. Dès lors, nous pouvons très bien imaginer d'utiliser ces algorithmes pour avoir une projection en deux dimensions de données non numériques telles que les cartes conceptuelles. Se pose alors la question de savoir comment calculer la distance entre deux cartes conceptuelles, et de manière plus générale entre deux ensembles (puisqu'une carte conceptuelle est un ensemble d'attributs).
M. Besson (Besson, 1973) propose de nombreuses méthodes pour calculer une distance entre deux ensembles, ou plus exactement entre deux parties A et B d'un ensemble E. Étudions deux d'entre elles.
4.2.1. Utilisation des vecteurs et fonctions caractéristiques
Une première façon de calculer une distance entre deux parties
A et B de E, tel que |E|=n, est de
représenter les parties (par exemple ici A) à l'aide d'un
vecteur ![]() de
{0,1}n tel que :
de
{0,1}n tel que :
avec
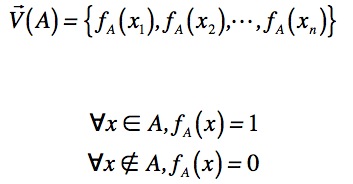
La distance d1 entre les deux parties A et B
de E revient alors à calculer la distance euclidienne entre
![]() et
et ![]() . Notons que cette
distance a été utilisée par F. Delorme
(Delorme et Loosli, 2006).
. Notons que cette
distance a été utilisée par F. Delorme
(Delorme et Loosli, 2006).
4.2.2. Distance basée sur la cardinalité des ensembles
Toutefois comme l'indique M. Besson (Besson, 1973), cette distance revient en fait à calculer la racine carrée de la cardinalité de la différence symétrique entre A et B, soit :
![]()
Pour rappel ![]() .
.
Cela signifie donc que seule la taille de la différence symétrique est prise en compte. Les tailles des ensembles A et B n'ont pas d'influence, ce qui risque de nous poser des problèmes car les cartes conceptuelles que crée un apprenant ont un nombre d'attributs variable.
Pour illustrer ce problème prenons l'exemple proposé par la figure 9. On a :
- A1 et A2 tels que ![]() ,
, ![]() et
et ![]()
- B1 et B2 tels que ![]() ,
, ![]() et
et ![]()
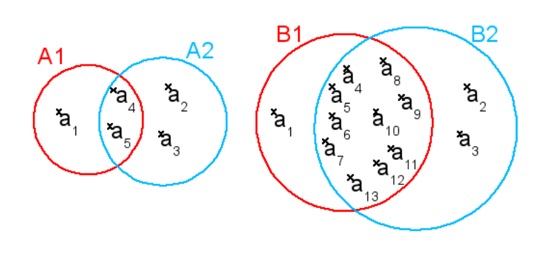
Figure 9 • Distance entre 2 ensembles
Ainsi la distance précédente nous dira que A1 est aussi proche de A2 que B1 est proche de B2, ce qui est intuitivement faux (la proportion d'attributs en commun entre B1 et B2 est nettement supérieure à A1 et A2).
M. Besson propose donc d'utiliser une distance d2 qui prend en compte la taille des deux ensembles en divisant la cardinalité de la différence symétrique par la cardinalité de l'union :
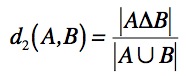
Alors que dans l'exemple précédent on avait ![]() on a maintenant :
on a maintenant :
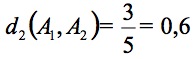
et
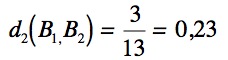
5. Représentation de traces
Dans cette partie nous allons montrer notre contribution répondant aux interrogations de la partie 3. Nous verrons tout d'abord quelles sont les données issues du logiciel Diogen que nous utiliserons pour créer des données interprétables. Nous montrerons ensuite comment nous avons adapté les algorithmes de la partie précédente pour afficher les chemins des apprenants.
5.1. Transformation d'actions élémentaires en ajout ou suppression d'attribut
Le logiciel Diogen enregistre certaines actions de l'utilisateur, plus exactement :
- le passage de la définition d'une notion à une autre (utilisation des onglets),
- l'ajout ou la suppression d'un concept sur la carte d'une notion à définir,
- l'ajout ou la suppression d'une relation sur la carte d'une notion à définir.

Figure 10 • Exemple d'actions enregitrées par le logiciel Diogen (format XML)
La figure 10 présente un extrait d'actions enregistrées par le logiciel Diogen (format XML). Toutefois isolées, ces informations n'ont pas beaucoup de signification : ce n'est pas parce qu'un apprenant a ajouté un concept sur la carte d'une notion à définir, qu'il va l'utiliser. Nous avons donc décidé de prendre en compte uniquement les actions qui modifient la définition que donne un apprenant d'une notion, c'est-à-dire les actions qui ajoutent ou qui retirent des attributs (nous rappelons qu'un attribut est composé d'une relation et d'un ou plusieurs concepts cibles). Les actions élémentaires sont regroupées, transformées et ordonnées/datées en actions explicites comme le montre la figure 11. Par la suite, nous appellerons trace d'un apprenant pour une notion à définir une suite de cartes conceptuelles datées, la première carte est la carte vide et la dernière est la carte de la solution proposée par l'apprenant.

Figure 11 • Exemples d'actions significatives (format XML)
5.2. Modification de la phase d'apprentissage des cartes de Kohonen
De part ses qualités de généralisation, les cartes de Kohonen semblent être l'outil idéal pour obtenir une représentation en deux dimensions des cartes conceptuelles.
Quelques propositions d'adaptation des cartes de Kohonen à des données symboliques ont été proposées, comme par exemple par A. El Golli et al. (El Golli et al, 2006). Cependant, aucune n'a répondu à notre attente, car notre problématique est un peu particulière. Dans notre cas, les données d'apprentissage sont des cartes conceptuelles (ou ensemble d'attributs) représentant uniquement des cartes finales d'enseignants. Cependant nos futures projections seront issues de cartes conceptuelles intermédiaires, donc par définition incomplètes. Par conséquent nos données d'apprentissage, même en ajoutant l'ensemble vide ne sont pas assez représentatives.
De plus la phase d'apprentissage des cartes de Kohonen « rapproche » des prototypes vers des valeurs intermédiaires aux valeurs d'apprentissage (Cf. figure 8). Dans notre cas cela se traduirait par rapprocher une ou plusieurs cartes d'une carte. Ce rapprochement consisterait à :
- combiner les cartes entres elles si elles sont de tailles égales,
- ajouter chaque attribut de la carte cible si elle est plus grande,
- supprimer un à un les attributs de la carte à rapprocher, si la carte cible est plus petite.
La conséquence est une explosion combinatoire du nombre de cartes produites. De plus, nombre de ces cartes n'ont pas de sens.
Nous proposons donc d'inverser ce fonctionnement en diffusant à partir des cartes d'apprentissages des cartes intermédiaires. Pour ce faire, à partir des neurones dont les prototypes sont les cartes d'apprentissage, nous diffusons des cartes possibles dans leur voisinage. Cette diffusion est obtenue en générant de nouvelles cartes par suppressions successives d'attributs en fonction de la distance au neurone source.
Dès lors, l'algorithme d'apprentissage d'une carte de Kohonen devient un algorithme d'initialisation (Cf. figure 12).

Figure 12 • Phase d'initialisation d'une carte de Kohonen de cartes conceptuelles
Précisons quelques points de cet algorithme :
- pour un neurone n de coordonnées (i,j), les cartes d'influence sont les cartes se trouvant dans le cercle de centre (i,j) et de rayon r. Ce rayon est par défaut fixé au nombre maximal d'attributs que possèdent les cartes d'apprentissage,
- le nombre d'attributs nbatt est fonction du nombre d'attributs que possèdent les cartes d'influence Ci que l'on décroît en fonction de la distance euclidienne entre (i,j) et les positions des cartes Ci.
Il est à noter que, tout comme pour A. El Golli et al. (El Golli et al, 2006), un prototype d'un neurone possède un ensemble de cartes. Mais dans notre cas la taille de cet ensemble peut varier d'un neurone à l'autre.
Pour projeter les futures cartes, il faut déterminer le neurone gagnant. Il faut donc pouvoir calculer une distance ou une dissimilarité entre un ensemble C de cartes et une carte c.
Deux cas se présentent :
- ![]() alors
l'idée est de pondérer la dissimilarité en fonction de la
cardinalité de C. Il faut de plus lorsque c est le seul
élément de C que cette dissimilarité soit
égale à 0 ;
alors
l'idée est de pondérer la dissimilarité en fonction de la
cardinalité de C. Il faut de plus lorsque c est le seul
élément de C que cette dissimilarité soit
égale à 0 ;
- ![]() dans ce cas, il
faut absolument que la dissimilarité soit plus grande que le cas
précédent.
dans ce cas, il
faut absolument que la dissimilarité soit plus grande que le cas
précédent.
Ceci nous oblige donc à utiliser un seuil pour calculer cette dissimilarité, seuil que nous avons fixé à 1. Nous obtenons la formule suivante :
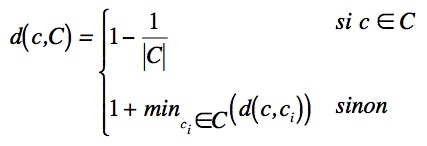
5.3. Positionnement initial des cartes d'apprentissage
Il nous faut maintenant associer certains neurones à nos cartes d'apprentissage. Or il est important que, lors de cette association, des cartes conceptuelles représentant les solutions d'un même exercice soient associées à des neurones proches. A contrario, les cartes conceptuelles représentant des solutions d'exercices différents doivent être représentées par des neurones assez éloignés.
Il nous faut donc une méthode d'association (de projection) qui conserve la proximité entre deux cartes conceptuelles. Mais il faut de plus que cette méthode n'ait besoin que d'une distance/similarité pour conserver cette propriété. Ces deux conditions sont remplies par l'algorithme SNE que nous avons vu précédemment.
Finalement, à l'image de ce que proposent Chien-Sing et Yashwant dans (Chien-Sing et Yashwant, 2004), nous allons utiliser successivement deux algorithmes de réduction de dimension. L'initialisation de notre carte de Kohonen passe par l'utilisation du SNE, pour identifier les neurones dont les prototypes seront les cartes des enseignants. Ensuite c'est l'algorithme de la figure 12 qui est exécuté pour générer les prototypes des neurones intermédiaires.
5.4. Choix des coordonnées pour le chemin d'un apprenant
Comme nous l'avons vu précédemment, les traces d'un apprenant
pour une notion donnée se résument à une liste de cartes,
commençant par la carte vide et finissant par la carte définissant
la notion. Par conséquent les coordonnées des points formant le
chemin d'un apprenant devraient donc être les projections de ces cartes
sur la carte de Kohonen que nous venons d'initialiser. Cependant lorsque l'on
essaye de déterminer le neurone gagnant pour une carte, nous n'obtenons
pas un neurone mais plusieurs neurones candidats : il faut donc en choisir un.
Il est à noter que ce problème n'est pas propre à notre
réseau de neurones. Mais alors que ce problème n'apparaît
que très rarement dans des cartes de Kohonen avec des données
issues de ![]() (bien que sur la
figure 8 il semble qu'il y ait plusieurs neurones susceptibles de dénoter
la couleur blanche) c'est un cas fréquent avec les cartes de Kohonen
utilisant des données (semi)-structurées
(El Golli et al, 2006).
(bien que sur la
figure 8 il semble qu'il y ait plusieurs neurones susceptibles de dénoter
la couleur blanche) c'est un cas fréquent avec les cartes de Kohonen
utilisant des données (semi)-structurées
(El Golli et al, 2006).
De plus, un apprenant ne définit pas uniquement une notion mais plusieurs, il va donc y avoir construction de plusieurs chemins. Logiquement tous ces chemins devraient partir du même point (la projection de la carte vide).
Ainsi nous avons décidé que la projection d'une carte conceptuelle sur la carte de Kohonen pourrait être contextualisée par des cordonnées (que l'on nomme « coordonnées contextes »). Dès lors si plusieurs neurones candidats ont été calculés pour une carte conceptuelle donnée, c'est celui dont les coordonnées sont les plus proches (au sens euclidien) des coordonnées contextes qui sera choisi.
Lors de la projection du premier point p0 (celui correspondant à la carte vide), les coordonnées contextes seront les coordonnées du barycentre des points d'apprentissage. Par la suite, les coordonnées du point pi (pour i>0) seront contextualisées par le point pi-1.
5.5. Validation à l'aide de données simulées
Avant de confronter nos algorithmes à des données réelles, nous les avons testés sur des données simulées.
5.5.1. Construction des données
Nous nous sommes placés dans un cadre idéal. Nous avons 9 notions à définir. Chaque notion est représentée par une carte « principale » composée de 4 attributs choisis au hasard parmi 200 disponibles. Afin de vérifier notre algorithme du SNE, nous avons généré des cartes « secondaires » proches des cartes principales : un des attributs a été changé aléatoirement par un autre. Par conséquent, chaque notion est représentée par 5 cartes différentes mais proches.
Ensuite nous avons considéré que nous avions un étudiant parfait qui construisait pour chaque notion la bonne carte. Et plus précisément, pour chaque notion nous sommes partis de la carte vide, auquel nous avons ajouté successivement les attributs de la carte principale.
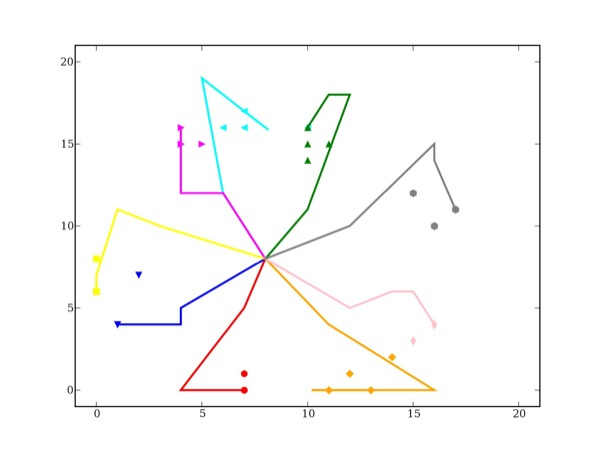
Figure 13 • Projection des traces à partir des données simulées
5.5.2. Validation
Nous avons exécuté nos algorithmes avec ces données en utilisant une carte de Kohonen de 400 neurones (20x20). Les résultats sont présentés à la figure 13.
Chaque couleur représente une notion à définir. Le résultat obtenu est le résultat escompté. Tout d'abord les zones des cartes des concepts sont bien identifiées, ce qui prouve que notre utilisation du SNE pour intialiser la carte de Kohonen est un bon choix. On peut toutefois remarquer que certaines cartes d'apprentissage se superposent. Cela est dû à la discrétisation des coordonnées de projection issue du SNE. Ensuite, les chemins de l'étudiant idéalement parfait tendent bien vers une des solutions et ne sont pas trop chaotiques, permettant donc une interprétation aisée.
5.6. Validation à l'aide de données réelles
Comme nous l'avons vu précédemment, lors des dernières utilisations du logiciel Diogen nous l'avions modifié pour qu'il enregistre toutes les actions. Nous avons utilisé, pour valider nos hypothèses, les résultats d'une expérimentation qui s'est déroulée en Mai 2005. Les apprenants devaient définir dix notions du cours sur la technologie RMI, qui sont : « Classe Stub », « Classe métier », « Client RMI », « Interface métier », « Objet distribué RMI », « Objet skeleton », « Objet stub », « Objet métier », « Serveur RMI » et « Service de nommage ».
Comme données d'apprentissage, l'enseignant a créé une carte par notion. Pour chaque notion nous avons enregistré les cartes intermédiaires de l'enseignant. Après avoir initialisé la carte de Kohonen selon notre algorithme, nous avons projeté ces cartes intermédiaires. La figure 14 montre la cohérence du résultat. Toutefois les chemins des notions représentés par les couleurs vertes (triangle pointe vers le haut) et rouge (rond) sont superposés.
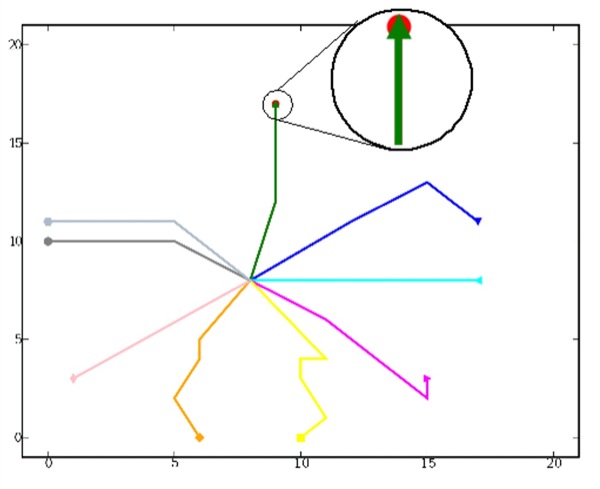
Figure 14 • Projection des traces réelles de l'enseignant
Prenons les traces d'un étudiant pour lequel la correction manuelle des cartes conceptuelles a donné de bons résultats (seules deux cartes ne sont pas acceptées par le correcteur). Le diagramme de la figure 15 présente les traces de cet étudiant. Malheureusement les résultats ne sont pas à la hauteur de nos attentes. On peut en effet constater que le nombre de chemins tendant vers les solutions ne reflète pas la correction manuelle. Quel est le problème ? Tout d'abord, le nombre de cartes de l'enseignant n'est pas suffisamment important. Ensuite, la projection sur la carte de Kohonen ne prend pas en compte la sémantique des attributs ou plutôt la proximité sémantique qu'il peut y avoir entre deux attributs. C'est ce que nous nous proposons d'améliorer.
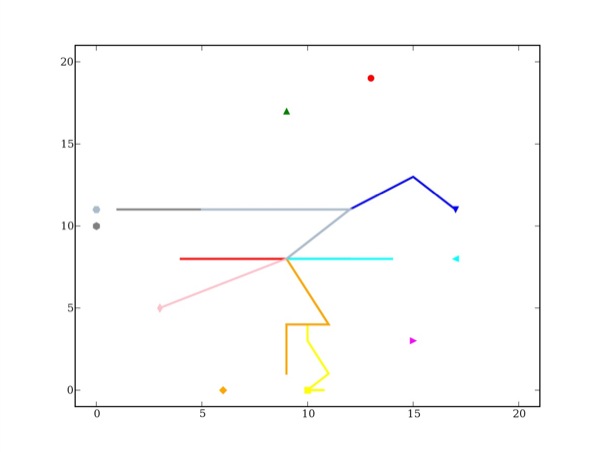
Figure 15 • Projection des traces réelles d'un « bon » apprenant
6. Amélioration en prenant en compte la similarité entre attributs
En analysant les productions de cet étudiant nous nous rendons compte qu'il a utilisé des attributs qui sont différents des attributs des cartes de référence, mais qui sont sémantiquement proches. Par exemple, l'enseignant pour définir la notion « classe métier », a utilisé l'attribut « étend RemoteServer » alors que l'apprenant a utilisé l'attribut « peut étendre RemoteServer ». Pour le système, ces attributs sont différents. Dans le calcul de la distance entre cartes, ils vont donc se retrouver dans le calcul de la cardinalité de la différence symétrique. Alors que pour un enseignant ces deux attributs sont presque équivalents. Comment prendre en compte cette similarité dans le calcul des distances entre cartes ?
6.1. Similarité entre attributs
Reprenons la formule qui nous permet de calculer la distance entre deux cartes conceptuelles C1 et C2 :
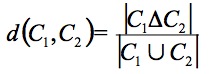
Il faudrait donc pondérer le numérateur lorsque des attributs sont sémantiquement proches. Nous pouvons obtenir cette information à partir du support utilisé pour construire les cartes conceptuelles. En effet, comme nous l'avons déjà vu, à l'image des graphes conceptuels, les concepts et les relations sont organisés hiérarchiquement par proximité sémantique (Cf. figure 3). Nous pouvons donc calculer la longueur du chemin qui permet d'aller d'un concept à un autre (idem pour les relations). Nous pouvons aussi normaliser cette distance en la divisant par la distance maximale qu'il peut y avoir entre deux concepts (respectivement entre deux relations). Par exemple la figure 16 propose un support composé de quatre concepts et de trois relations. La distance entre les concepts c1 et c3 est alors de 1, et celle entre les relations r1 et r2 est de 2/3.
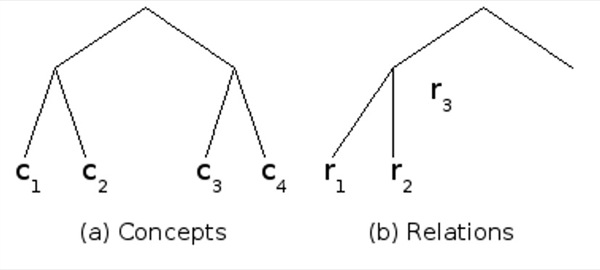
Figure 16 • Hiérarchies de concepts et de relations
Nous pouvons alors calculer une distance entre attributs comprise entre 0 et 1 en calculant la moyenne des distances entre les deux concepts et entre les deux relations. Ainsi le tableau 1 présente les distances entre tous les attributs créés à partir du support de la figure 16.
|
|
ac1,r1 |
ac1,r2 |
ac1,r3 |
ac2,r1 |
ac2,r2 |
ac2,r3 |
ac3,r1 |
ac3,r2 |
ac3,r3 |
ac4,r1 |
ac4,r2 |
ac4,r3 |
|
ac1,r1 |
0 |
0,33 |
0,5 |
0,25 |
0,58 |
0,75 |
0,5 |
0,83 |
1 |
0,5 |
0,83 |
1 |
|
ac1,r2 |
0,33 |
0 |
0,33 |
0,58 |
0,25 |
0,58 |
0,83 |
0,5 |
0,83 |
0,83 |
0,5 |
0,83 |
|
ac1,r3 |
0,5 |
0,33 |
0 |
0,75 |
0,58 |
0,25 |
1 |
0,83 |
0,5 |
1 |
0,83 |
0,5 |
|
ac2,r1 |
0,25 |
0,58 |
0,75 |
0 |
0,33 |
0,5 |
0,5 |
0,83 |
1 |
0,5 |
0,83 |
1 |
|
ac2,r2 |
0,58 |
0,25 |
0,58 |
0,33 |
0 |
0,33 |
0,83 |
0,5 |
0,83 |
0,83 |
0,5 |
0,83 |
|
ac2,r3 |
0,75 |
0,58 |
0,25 |
0,5 |
0,33 |
0 |
1 |
0,83 |
0,5 |
1 |
0,83 |
0,5 |
|
ac3,r1 |
0,5 |
0,83 |
1 |
0,5 |
0,83 |
1 |
0 |
0,33 |
0,5 |
0,25 |
0,58 |
0,75 |
|
ac3,r2 |
0,83 |
0,5 |
0,83 |
0,83 |
0,5 |
0,83 |
0,33 |
0 |
0,33 |
0,58 |
0,25 |
0,58 |
|
ac3,r3 |
1 |
0,83 |
0,5 |
1 |
0,83 |
0,5 |
0,5 |
0,33 |
0 |
0,75 |
0,58 |
0,25 |
|
ac4,r1 |
0,5 |
0,83 |
1 |
0,5 |
0,83 |
1 |
0,25 |
0,58 |
0,75 |
0 |
0,33 |
0,5 |
|
ac4,r2 |
0,83 |
0,5 |
0,83 |
0,83 |
0,5 |
0,83 |
0,58 |
0,25 |
0,58 |
0,33 |
0 |
0,33 |
|
ac4,r3 |
1 |
0,83 |
0,5 |
1 |
0,83 |
0,5 |
0,75 |
0,58 |
0,25 |
0,5 |
0,33 |
0 |
Tableau 1 • Exemple de calcul de distance entre attributs
6.2. Nouveau calcul de dissimilarité entre cartes conceptuelles
Maintenant que nous avons la possibilité de calculer une distance entre deux attributs, distance qui est comprise entre 0 et 1, nous pouvons modifier le calcul de dissimilarité entre deux cartes conceptuelles. Nous parlons maintenant de dissimilarité car nous n'avons pas vérifié que notre proposition valide l'inégalité triangulaire (condition indispensable dans le cadre d'une distance).
Il faudrait lorsque deux attributs sont éloignés sémantiquement que l'on retrouve la formule précédente. Or lorsque deux attributs sont éloignés, leur distance a pour valeur 1. Dans la formule précédente ces deux attributs apparaissent dans le numérateur car ce sont des éléments de la différence symétrique, ils augmentent donc la valeur de cette cardinalité de 2. Cette réflexion induit l'algorithme présenté à la figure 17 pour calculer le nouveau numérateur.
Le principe est, lorsqu'aucune des deux cartes n'est vide, de sélectionner deux attributs a et b (avec a appartenant à la première carte et b à la seconde) qui sont les plus proches (qui minimisent donc leur distance). Dans ce cas le numérateur de la distance entre les deux cartes est égal à deux fois la distance de a à b en additionnant le résultat de l'application de ce même algorithme avec les deux cartes ne possédant plus a et b.

Figure 17 • Calcul du numérateur de la distance entre deux cartes (CalcNum)
Finalement nous avons :
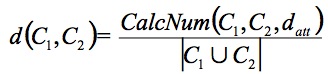
Pour bien comprendre ce calcul, reprenons l'exemple précédent en supposant que l'on désire calculer la distance entre deux cartes C1 et C2 telles que :
- C1 est composée des attributs ac1,r1 , ac2,r1 et ac3,r3;
- C2 est composée des attributs ac2,r2 et ac4,r1.
Les distances entre ces attributs présentées par le tableau 2 sont extraites du tableau 1. Ainsi, pour calculer la distance entre C1 et C2, on commence par rechercher la plus petite distance entre deux attributs, en l'occurrence celle entre ac2,r1 et ac2,r2, soit 0,33. Une fois ces deux attributs retirés, c'est la distance entre ac1,r1 et ac4,r1 qui est la plus petite, soit 0,5 Il ne reste alors plus que l'attribut ac3,r3 de la carte C1 qui n'a pas été utilisé. Dès lors, on a :
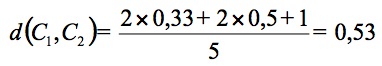
alors qu'avec la distance précédente nous aurions obtenue la valeur 1.
|
|
ac1,r1 |
ac2,r1 |
ac3,r3 |
|
ac2,r2 |
0,58 |
0,33 |
0,83 |
|
ac4,r1 |
0,5 |
0,5 |
0,75 |
Tableau 2 • Distance entre attributs des cartes C1 et C2
6.3. Validation
Avant de valider cette nouvelle proposition avec les productions des apprenants, reprenons la production de l'enseignant (Cf. figure 18). Nous pouvons constater que le résultat est celui attendu. En effet, la progression des chemins de l'enseignant le mène bien aux solutions qu'il a lui-même définies. De plus, les solutions et les chemins sont discriminés contrairement à nos précédents tests.
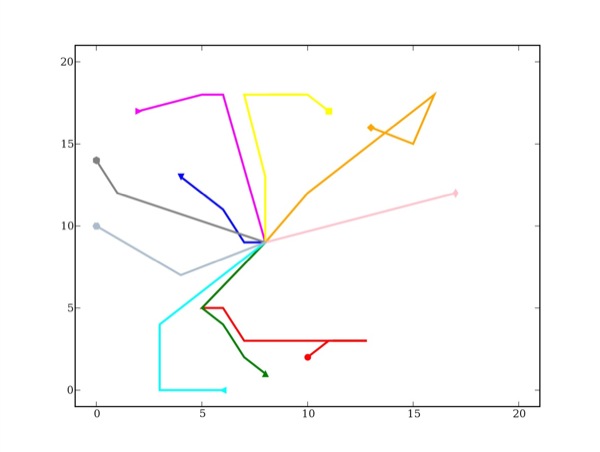
Figure 18 • Nouvelle projection des traces réelles de l'enseignant avec calcul de similarité entre attributs
Nous avons aussi validé cette nouvelle approche avec les données récupérées lors de l'expérimentation de Mai 2005, soit avec les traces de 22 apprenants.
Le diagramme de la figure 19 est la nouvelle projection de l'apprenant précédent. Bien qu'un peu plus confus au premier abord, les chemins sont mieux séparés les uns des autres. On peut noter qu'il a mal défini les notions représentées par les couleurs gris foncé (hexagone) et magenta (triangle pointe à droite) : soit les deux notions qui avaient été notées fausses lors de la correction manuelle. Sinon, à part quelques hésitations (chemins gris clair et vert), on voit que les autres chemins tendent vers la bonne direction.
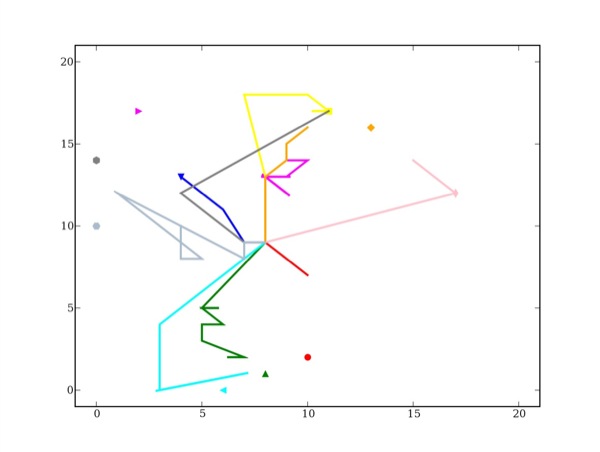
Figure 19 • Nouvelle projection des traces réelles d'un « bon » apprenant avec calcul de similarité entre attributs
Le diagramme de la figure 20 quant à lui présente la projection d'un apprenant en grande difficulté. Les chemins sont chaotiques, changent régulièrement de direction (chemins vert, magenta et rose) et certains ne vont pas dans la bonne direction (chemins rouge et bleu). En observant la construction de ces chemins, l'enseignant devrait rapidement se rendre compte qu'il y a un problème avec cet apprenant et donc pouvoir intervenir au plus tôt.
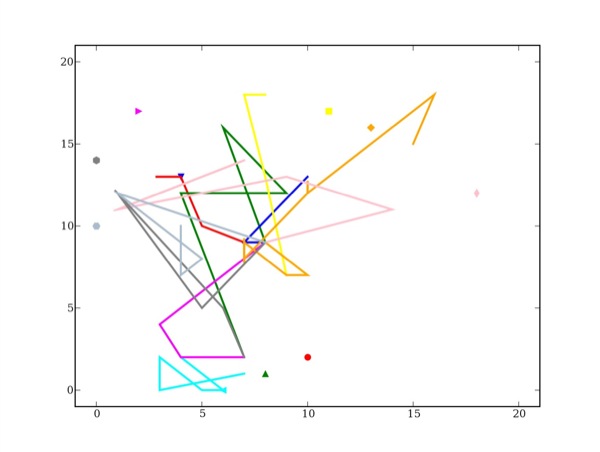
Figure 20 • Projection des traces réelles d'un apprenant en difficulté avec calcul de similarité entre attributs
7. Conclusions et perspectives
Nous avons dans cet article décrit une nouvelle interface, ainsi qu'une nouvelle méthode pour évaluer la progression d'un étudiant résolvant un exercice. Contrairement à un outil comme CourseVis (Mazza et Dimitrova, 2007), qui utilise uniquement une signalétique de couleur donnant uniquement l'état de la production de l’apprenant à un instant t, nous avons développé un outil permettant de caractériser le résultat aussi bien en terme d'avancement qu'en terme d'exactitude. Pour cela nous avons créé des algorithmes originaux, dont une nouvelle manière d'initialiser les cartes de Kohonen lorsque les données sont symboliques. De plus, nous avons validé la cohérence des résultats sur des données réelles d'une promotion de 22 étudiants.
Toutefois cette validation, pour le moment, ne prend pas en compte la communauté enseignante dans la pratique de l'outil. Nous sommes conscients qu'un des problèmes de notre approche est le suivi d'un nombre important d'apprenants. Il faudrait au préalable fournir à l'enseignant une vue globale et synthétique de l'avancement des apprenants pour l'aider à choisir les traces de l'apprenant qu'il veut visualiser.
C'est ce que propose CourseVis via une matrice de couleurs pour présenter cette vue synthétique. Nous pourrions alors connecter notre outil pour obtenir le fonctionnement de la figure 21. Mais une fois de plus avec CourseVis, nous retombons sur une observation globale des étudiants sans même connaître leur dynamique. L'étudiant passe-t-il du vert au rouge parce qu'il est lent, parce qu'il se trompe et comment se trompe-t-il ? Il n'y a pas de dynamique de comportement dans l'outil.

Figure 21 • Les 3 étapes de détection et de suivi d'un apprenant
Une de nos principales perspectives est de généraliser notre outil à l'observation d'une classe. L'idée n'est plus de calculer des distances entre la carte de l'étudiant et la carte solution pour chaque exercice d'un devoir. Nous considérerons le devoir comme un ensemble de cartes d'exercices et nous calculerons les distances entre l'ensemble des cartes de l'étudiant et l'ensemble des cartes solution du devoir.
Lorsque nous aurons cet outil de synthèse, une autre perspective sera la validation de ces travaux par une mise en oeuvre dans des conditions temps réel avec des enseignants. Nous savons déjà que les algorithmes que nous utilisons ne poseront pas de problème. En effet, l'algorithme le plus gourmand en temps est l'algorithme du SNE (à cause de l'algorithme de descente de gradient). Mais ce dernier n'est lancé qu'une seule fois pour initialiser la carte de Kohonen. Ensuite la projection d'une carte ne prend que quelques dixièmes de seconde.
D'une manière plus générale, notre méthode est applicable à toutes données modélisables par des ensembles et pour lesquelles on peut établir une similarité. De plus il est nécessaire d’avoir des exemples d’apprentissage (dans notre cas des cartes solutions des exercices). Par exemple, notre méthode est applicable sur les données présentées par Harp et al. (Harp et al, 1995). Celui-ci montre en effet comment transformer des données symboliques issues de QCM en ensembles organisés de connaissances.
Nous espérons grâce à ces algorithmes et à ces outils pouvoir améliorer le suivi en temps réel d'étudiants à distance.
Remerciements
Nous tenons ici à remercier Alain Rakotomamonjy et Gilles Gasso pour toute l'aide qu'ils nous ont apportée lors de l'étude des algorithmes de classification et des algorithmes de réduction de dimensions.
BIBLIOGRAPHIE
BART B.-M.. (1993). Le savoir en construction. Retz.
BESSON M. (1973) A propos des distances entre ensembles de parties. Mathématiques et Sciences Humaines, 42 p.17–35.
BlOOM B. S. (1956) Taxonomy of Educational Objectives, Handbook I : The Cognitive Domain. David McKay Co Inc.
COVER T., P. Hart. (1967) Nearest neighbor pattern classification. Information Theory, IEEE Transactions, vol. 13 p. 21–27.
CHIEN-SING L., YASHWANT P. S. (2004) Student modeling using principal component analysis of som clusters. In Proceedings of the IEEE International Conference on Advanced Learning Technologies, p. 480 – 484. IEEE Computer Society.
DELORME F., (2005) Évaluation et modélisation automatiques des connaissances des apprenants à l’aide de cartes conceptuelles. Thèse, INSA de Rouen.
DELORME F., LOOSLI G., (2006) Un outil générique pour l’analyse automatique et la visualisation de productions d’apprenants. In TICE 2006, Technologies de l’Information et de la Communication dans les Enseignements.
EL GOLLI A., ROSSI F., CONAN-GUEZ B., LECHEVALLIER Y., (2006) Une adaptation des cartes auto-organisatrices pour des données décrites par un tableau de dissimilarités. Revue de Statistique Appliquée, LIV(3) p. 33–64,.
GENEST D., (2002) Recherche d’information par transformation de graphes dans le modèle des graphes conceptuels. Ingénierie des systèmes d’information,7(1-2) p. 207–236.
HARP S. A., SAMAD T., VILLANO M., (1995) Modeling student knowledge with self-organizing feature maps. IEEE transactions on systems, man, and cybernetics, 25(5) p. 727–737.
HOTELLING H., (1933) Analysis of a complex of statistical variables with principal components. Journal of Educational Psychology.
HINTON G., ROWEIS S., (2003) Stochastic neighbor embedding. In S. Thrun S. Becker and K. Obermayer, editors, Advances in Neural Information Processing Systems vol 15, p. 833–840. MIT Press.
KOHONEN T., (2001) Self-Organizing Maps. Springer, Verlag.
LABAT J.-M. (2002) Eiah, quel retour d’informations pour le tuteur ? In Technologies de l’Information et de la Communication dans les Enseignements d’ingénieurs et dans l’industrie, p. 81–88.
LEBART L., MORINEAU A., FENELON J.-P., (1982) Traitement des données statistiques. Dunod Ed.
MAZZA R., DIMITROVA V., (2007) Coursevis : A graphical student monitoring tool for supporting instructors in web-based distance courses. International Journal in Human-Computer Studies, (65) p. 125–139.
PREUX P., (2007) Fouille de données, notes de cours. Disponible sur internet http://www.grappa.univ-lille3.fr/˜ppreux/, ( avril 2007).
ROWEIS S. T., Saul L. K., (2000) Nonlinear dimensionality reduction by locally linear embedding. Science, 290(5500) p. 2323 – 2326.
VAN DER MAATEN L., (2007) Dimensionality reduction : A comparative review. Disponible sur internet consulté en mai 2007) http://www.cs.unimaas.nl/l.vandermaaten/Laurens_van_der_Maaten/Matlab_Toolbox _for_Dimensionality_Reduction.html.
 A
propos des auteurs
A
propos des auteurs
Nicolas DELESTRE est Maître de Conférences
à l'INSA de Rouen. Il est membre du LITIS (Laboratoire d'Informatique, de
Traitement de l'Information et des Systèmes). Il enseigne
l'algorithmique, les réseaux et l'informatique répartie dans le
département ASI.
Il a soutenu sa thèse début 2000 en Informatique dans le
domaine des hypermédias adaptatifs dynamiques. Depuis cette thèse
il s'est spécialisé dans le domaine de l'évaluation des
apprenants à l'aide d'algorithmes d'apprentissage. Dans ce cadre, il a
co-encadré avec Jean-Pierre Pécuchet les travaux de thèse
de Fabien Delorme. Il est aussi membre du groupe de l'AFNOR qui travaille sur la
normalisationde métadonnées pour les ressources
pédagogiques.
Adresse : INSA de Rouen, Campus de Saint-Étienne du Rouvray, Avenue de l’Université - BP 8 76801 Saint-Étienne-du-Rouvray Cedex
Courriel : Nicolas.Delestre@insa-rouen.fr
Nicolas MALANDAIN est Maître de Conférences
à l'INSA de Rouen. Il est membre du LITIS (Laboratoire d'Informatique, de
Traitement de l'Information et des Systèmes). Il enseigne la
programmation JAVA, l'architecture des ordinateurs et les systèmes
d'exploitation, les technologies web et les interactions homme-machine.
Il a soutenu sa thèse en 2001 en Informatique dans le domaine de
l'extraction et l'interprétation d'informations géographiques dans
des documents ainsi que leur mise en relation avec des cartes.
Adresse : INSA de Rouen, Campus de Saint-Étienne du Rouvray, Avenue de l’Université - BP 8 76801 Saint-Étienne-du-Rouvray Cedex
Courriel : Nicolas.Malandain@insa-rouen.fr
Nicolas DELESTRE, Nicolas MALANDAIN, Analyse et représentation en deux dimensions de traces pour le suivi de l'apprenant, Revue STICEF, Volume 14, 2007, ISSN : 1764-7223, mis en ligne le 12/03/2008, http://sticef.org
© Revue Sciences et Technologies de l´Information et de la Communication pour l´Éducation et la Formation, 2007